Repaso de funciones

En esta clase, vamos a revisar las características de las funciones más utilizadas en matemática

---

Objetivos de la clase:

1. Recordar las características básicas de las funciones más utilizadas en 2° año de bachillerato:
   • Función lineal
   • Función valor absoluto
   • Función cuadrática
   • Funciones polinómicas
   • Función exponencial
   • Función logarítmica
   • Función racional
   • Función radical con índice par e impar
2. Revisar las gráficas y las ecuaciones que representan cada una de las funciones listadas en el numeral 1

---

Contenidos:

1. Función lineal
2. Función valor absoluto
3. Función cuadrática
4. Funciones polinómicas
5. Función exponencial
6. Función logarítmica
7. Función racional
8. Función radical con índice par e impar

---

Actividades:

Vamos a ver los repasos de las siguientes funciones:

FUNCIÓN LINEAL

• Definición Formal:
  • Una función lineal es una relación entre dos variables (generalmente representadas por x e y) donde a cada valor de x le corresponde un único valor de y, y su representación gráfica es una línea recta.
  • Ejemplo: y = 2x + 3. En esta ecuación, a cada valor de x le corresponde un único valor de y, calculado multiplicando x por 2 y sumando 3.
• Representación Gráfica:
  • La gráfica de una función lineal siempre es una línea recta en el plano cartesiano.
  • La pendiente de la recta determina su inclinación, mientras que la ordenada al origen indica el punto donde la recta corta al eje y.

Forma de la ecuación Pendiente-Ordenada (PO)

Donde:

• m: Pendiente de la recta (indica la inclinación).
• b: Ordenada al origen (punto donde la recta corta al eje y).

Pendiente (m)

La pendiente es una medida de qué tan inclinada está una recta.

• Pendiente positiva: La recta se inclina hacia arriba de izquierda a derecha.
• Pendiente negativa: La recta se inclina hacia abajo de izquierda a derecha.
• Pendiente cero: La recta es horizontal.
• Pendiente indefinida: La recta es vertical.

¿Cómo se obtiene la pendiente de una recta?

1. A partir de la gráfica:

• Identifica dos puntos cualesquiera sobre la recta. Llamémosles (x₁, y₁) y (x₂, y₂).
• Calcula la diferencia de las ordenadas (valores de y): y₂ – y₁.
• Calcula la diferencia de las abscisas (valores de x): x₂ – x₁.
• La pendiente (m) es el cociente entre estas diferencias: m = (y₂ – y₁) / (x₂ – x₁).

2. A partir de la ecuación:

• Forma pendiente-ordenada: Si la ecuación de la recta está en la forma y = mx + b, el coeficiente de x (la letra m) es directamente la pendiente.

3. A partir de dos puntos:

• Utiliza la fórmula: m = (y₂ – y₁) / (x₂ – x₁).
  • Ejemplo: Si tienes los puntos (2, 5) y (4, 9), la pendiente sería: m = (9 – 5) / (4 – 2) = 4 / 2 = 2.

Ejemplo Visual:

¿Qué nos indica la pendiente?

• Inclinación de la recta:
  • Pendiente positiva (m > 0): La recta sube de izquierda a derecha.
  • Pendiente negativa (m < 0): La recta baja de izquierda a derecha.
  • Pendiente cero (m = 0): La recta es horizontal.
  • Pendiente indefinida (m = ∞): La recta es vertical.
• Tasa de cambio: Indica cuánto cambia el valor de y por cada unidad que aumenta x.

Ejemplo práctico:

Imagina que estás en un auto y viajas a una velocidad constante. La distancia recorrida (y) depende del tiempo transcurrido (x). Si graficamos esta relación, obtendremos una línea recta. La pendiente de esta recta representará la velocidad del auto, es decir, cuántos kilómetros recorres por cada hora.

¿Quieres practicar?

Aquí tienes algunos ejercicios:

1. Calcula la pendiente de una recta que pasa por los puntos (3, -2) y (5, 4).
2. Dada la ecuación y = -2x + 1, ¿cuál es la pendiente de la recta?
3. ¿Qué tipo de recta tiene una pendiente igual a cero? ¿Y una pendiente indefinida?

Pregunta para el Alumno:

¿Pueden pensar en algún ejemplo de una situación real donde una función lineal podría ser utilizada?

Diferentes Formas de la Ecuación de una Recta

1. Forma pendiente-ordenada (PO):

• Ecuación: y = mx + b
• Elementos:
  • m: Pendiente de la recta (inclinación).
  • b: Ordenada al origen (punto donde la recta corta al eje y).
• Ventajas: Es la forma más común y fácil de interpretar. La pendiente y la ordenada al origen se identifican directamente.

2. Forma punto-pendiente (PP):

• Ecuación: y – y₁ = m(x – x₁)
• Elementos:
  • m: Pendiente de la recta.
  • (x₁, y₁): Un punto que pertenece a la recta.
• Ventajas: Útil cuando se conoce la pendiente y un punto de la recta.

3. Forma general:

• Ecuación: Ax + By + C = 0
• Elementos:
  • A, B, C: Coeficientes numéricos.
• Ventajas: Es una forma general que incluye todas las rectas, incluso las verticales.

4. Forma simétrica:

• Ecuación: x/a + y/b = 1
• Elementos:
  • a: Intersección con el eje x.
  • b: Intersección con el eje y.
• Ventajas: Útil cuando se conocen las intersecciones con los ejes.

¿Cuándo usar cada forma?

• Forma pendiente-ordenada (PO): Ideal para graficar rápidamente y para entender el comportamiento de la recta.
• Forma punto-pendiente (PP): Útil cuando se tiene un punto y la pendiente, o cuando se quiere encontrar la ecuación de una recta paralela o perpendicular a otra.
• Forma general: Se utiliza en sistemas de ecuaciones lineales y en geometría analítica.
• Forma simétrica: Es útil cuando se conocen las intersecciones con los ejes y se quiere encontrar la ecuación de una recta que pasa por dos puntos dados.

Relación entre las formas

Todas estas formas son equivalentes y se pueden transformar de una a otra mediante operaciones algebraicas. Por ejemplo, la forma punto-pendiente se puede transformar en la forma pendiente-ordenada despejando y.

Ejemplo:

Dada la recta que pasa por los puntos (2, 3) y (5, 9):

• Encontrar la pendiente: m = (9 – 3) / (5 – 2) = 2.
• Usar la forma punto-pendiente: y – 3 = 2(x – 2).
• Transformar a la forma pendiente-intersección: y = 2x – 1.

Aplicaciones de las rectas en la vida real

1. Física:

• Movimiento rectilíneo uniforme: La trayectoria de un objeto que se mueve a velocidad constante se representa mediante una recta en un gráfico de posición vs. tiempo.
• Ley de Ohm: La relación entre el voltaje, la corriente y la resistencia en un circuito eléctrico se representa mediante una recta.
• Gráficas de fuerzas: Muchas fuerzas, como la fuerza de gravedad o la fuerza elástica, se representan gráficamente como rectas.

2. Ingeniería:

• Diseño de estructuras: Las rectas se utilizan para diseñar vigas, columnas y otros elementos estructurales en edificios, puentes y máquinas.
• Cálculo de pendientes: En topografía, se utilizan las rectas para calcular la pendiente de un terreno y diseñar carreteras, canales y otras infraestructuras.
• Cinemática: El movimiento de los objetos se describe mediante ecuaciones lineales, que representan gráficamente rectas.

3. Economía:

• Oferta y demanda: La relación entre la cantidad demandada de un producto y su precio se representa a menudo mediante rectas.
• Análisis de costos: Los costos fijos y variables de una empresa se pueden representar gráficamente como rectas.
• Crecimiento económico: Las tasas de crecimiento económico a corto plazo se pueden aproximar mediante rectas.

4. Estadística:

• Regresión lineal: Se utiliza para modelar la relación entre dos variables cuantitativas. La recta de regresión representa la tendencia general de los datos.
• Análisis de series de tiempo: Las tendencias lineales se utilizan para analizar cómo cambian las variables a lo largo del tiempo.

5. Otras áreas:

• Cartografía: Las líneas rectas se utilizan para representar carreteras, ríos y otras características geográficas en mapas.
• Diseño gráfico: Las líneas rectas son un elemento fundamental en el diseño de logotipos, carteles y otros materiales visuales.
• Programación: Las rectas se utilizan en algoritmos de gráficos y en la programación de robots.

Ejemplos concretos:

• Un termómetro: La escala de un termómetro es una recta que relaciona la temperatura con la altura de la columna de mercurio.
• Una rampa: La pendiente de una rampa determina su inclinación y se calcula utilizando la ecuación de una recta.
• Una factura de teléfono: El costo total de una factura de teléfono móvil suele ser una función lineal del número de minutos utilizados.

¿En qué área te gustaría profundizar más? Podemos explorar ejemplos más específicos o resolver problemas relacionados con las aplicaciones de las rectas.

Algunas preguntas que podríamos abordar:

• ¿Cómo se utiliza la pendiente de una recta para calcular la velocidad de un objeto?
• ¿Qué significa la intersección con el eje y en una gráfica de oferta y demanda?
• ¿Cómo se puede utilizar la regresión lineal para predecir el precio de una vivienda?

Conclusiones

La función lineal es una herramienta matemática fundamental que describe relaciones directas entre variables, donde la pendiente representa la tasa de cambio constante. Entender su significado y uso es clave para interpretar datos y resolver problemas en múltiples campos, desde la economía hasta la física. Al conocer la pendiente, se pueden predecir tendencias y tomar decisiones informadas. Sus aplicaciones prácticas son vastas, evidenciando su relevancia en la vida cotidiana y en diversas disciplinas científicas y tecnológicas.

FUNCIÓN VALOR ABSOLUTO

¿Qué es el valor absoluto?

Imagina una recta numérica. El valor absoluto de un número es simplemente su distancia desde el cero, sin importar si el número es positivo o negativo. Por ejemplo, el valor absoluto de 5 y de -5 es 5, ya que ambos números están a una distancia de 5 unidades del cero.

Notación: Se representa con dos barras verticales: |x|.

La función valor absoluto

Una función valor absoluto es aquella que involucra el valor absoluto de una expresión algebraica. Por ejemplo: f(x) = |x + 2|.

Gráfica de la función valor absoluto

La gráfica de una función valor absoluto tiene forma de “V”. El vértice de la V se encuentra en el punto donde la expresión dentro del valor absoluto es igual a cero.

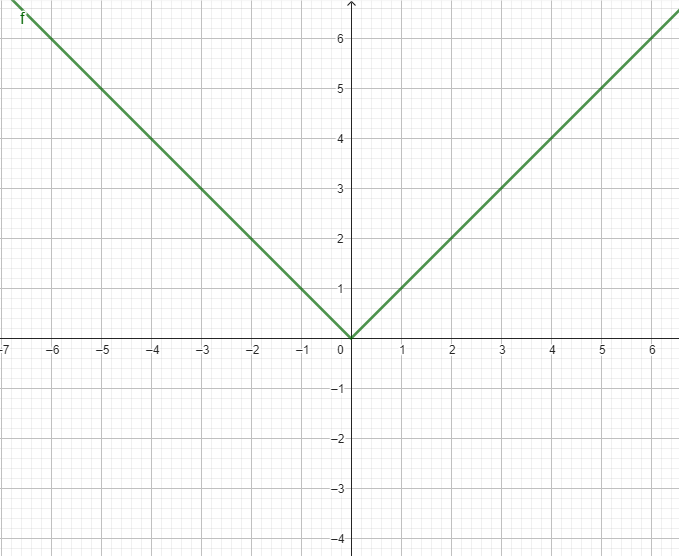
Propiedades de la función valor absoluto

• Siempre positiva o cero: El valor absoluto de cualquier número es siempre mayor o igual a cero.
• Simétrica respecto al eje y: La gráfica de una función valor absoluto es simétrica respecto al eje y.

Cómo construir la gráfica de una función valor absoluto

1. Encuentra el vértice: Resuelve la ecuación dentro del valor absoluto igual a cero para encontrar la coordenada x del vértice. La coordenada y del vértice será el valor absoluto de la expresión evaluada en ese punto.
2. Elige valores de x a ambos lados del vértice: Calcula los valores correspondientes de y y grafica los puntos.
3. Une los puntos: Traza una línea recta a partir del vértice hacia cada uno de los puntos que graficaste.

Aplicaciones prácticas del valor absoluto

• Distancia: El valor absoluto se utiliza para calcular distancias en la recta numérica y en el plano cartesiano.
• Errores: En física y otras ciencias, el valor absoluto se utiliza para medir errores y tolerancias.
• Optimización: En problemas de optimización, el valor absoluto se puede utilizar para minimizar o maximizar ciertas cantidades.
• Programación: El valor absoluto se utiliza en algoritmos de programación para calcular distancias y resolver problemas geométricos.

Ejemplos y ejercicios

• Graficar: f(x) = |x – 3| + 2
• Resolver ecuaciones: |2x – 1| = 5
• Aplicaciones: Un termómetro marca una temperatura de -5°C. ¿Cuál es la diferencia entre la temperatura actual y la temperatura ideal de 20°C?

Actividades interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes funciones valor absoluto y sus propiedades.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la gráfica de una función valor absoluto al modificar los parámetros.

Conclusión

La función valor absoluto es una herramienta matemática muy versátil con numerosas aplicaciones en diferentes campos. Comprender sus propiedades y cómo graficarlas te permitirá resolver una amplia variedad de problemas.

FUNCIÓN CUADRÁTICA

¿Qué es una Función Cuadrática?

Una función cuadrática es una función polinómica de segundo grado. Su forma general es:

f(x) = ax² + bx + c

Donde:

• a, b y c son números reales, y a es diferente de cero.
• La gráfica de una función cuadrática es una parábola.

Características de la Parábola

• Vértice: Punto máximo o mínimo de la parábola.
• Eje de simetría: Línea vertical que divide a la parábola en dos partes simétricas.
• Concavidad: Indica si la parábola abre hacia arriba (a > 0) o hacia abajo (a < 0).
• Intersecciones con los ejes: Puntos donde la parábola corta al eje x y al eje y.

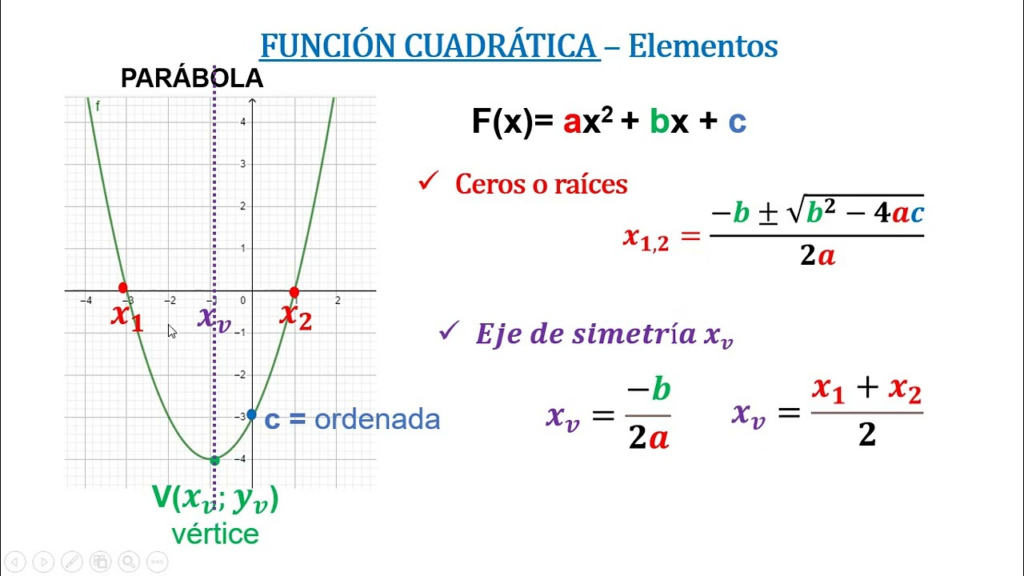
Ecuación Canónica

La ecuación canónica de una parábola es una forma alternativa de expresar la función cuadrática que facilita la identificación del vértice:

f(x) = a(x - h)² + k

Donde:

• (h, k) son las coordenadas del vértice.

Vértice y Eje de Simetría

• Vértice: El vértice de una parábola es el punto (h, k) en la ecuación canónica.
• Eje de simetría: Es la recta vertical que pasa por el vértice. Su ecuación es x = h.

Intersecciones con los Ejes

• Intersección con el eje y: Se obtiene sustituyendo x = 0 en la ecuación de la función. El punto de corte es (0, c).
• Intersección con el eje x: Se obtiene resolviendo la ecuación cuadrática f(x) = 0.

Transformación de Ecuaciones

Podemos transformar la ecuación general a la forma canónica completando el cuadrado.

Observemos los siguientes videos:

Después de ver el video, realiza las siguientes actividades:

1. Ejercicio 1: Pasar la ecuación general de la parábola y=2×2−8x+5 a la forma canónica y encontrar su vértice, eje de simetría e intersecciones con los ejes.
2. Ejercicio 2: Dada la ecuación canónica de la parábola y=−3(x−2)2+4, encontrar su ecuación general y graficar la parábola.
3. Ejercicio 3: Resolver el siguiente problema de aplicación: Un proyectil es lanzado desde el suelo con una velocidad inicial de 20 m/s y un ángulo de elevación de 45°. La ecuación que describe la trayectoria del proyectil es y=−4.9×2+20x. ¿Cuál es la altura máxima alcanzada por el proyectil? ¿A qué distancia del punto de lanzamiento cae el proyectil?

Ahora observemos este otro video:

Luego de ver el video, realizar estas actividades:

1. Ejercicio 1: Pasar la ecuación general de la parábola y=2×2−8x+5 a la forma canónica y encontrar su vértice, eje de simetría e intersecciones con los ejes.
2. Ejercicio 2: Dada la ecuación canónica de la parábola y=−3(x−2)2+4, encontrar su ecuación general y graficar la parábola.
3. Ejercicio 3: Resolver el siguiente problema de aplicación: Un proyectil es lanzado desde el suelo con una velocidad inicial de 20 m/s y un ángulo de elevación de 45°. La ecuación que describe la trayectoria del proyectil es y=−4.9×2+20x. ¿Cuál es la altura máxima alcanzada por el proyectil? ¿A qué distancia del punto de lanzamiento cae el proyectil?

Aplicaciones de las Funciones Cuadráticas

• Física: Movimiento de proyectiles, trayectorias parabólicas.
• Ingeniería: Diseño de puentes, antenas parabólicas.
• Economía: Modelos de oferta y demanda, maximización de beneficios.

Ejemplos y Ejercicios

1. Graficar: f(x) = x² – 4x + 3
2. Encontrar el vértice: f(x) = -2x² + 8x – 5
3. Hallar las intersecciones con los ejes: f(x) = x² – 5x
4. Transformar a la forma canónica: f(x) = 2x² + 12x + 10

Actividades Interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes funciones cuadráticas y sus propiedades.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la parábola al modificar los valores de a, b y c.

Conclusión

La función cuadrática es una herramienta matemática fundamental con numerosas aplicaciones en diferentes campos. Comprender sus propiedades y cómo graficarlas te permitirá resolver una amplia variedad de problemas.

FUNCIONES POLINÓMICAS

¿Qué es una Función Polinómica?

Una función polinómica es una función que se expresa como la suma de potencias enteras no negativas de una variable, multiplicadas por coeficientes constantes. Su forma general es:

f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀

Donde:

• n es un número entero no negativo y se llama grado del polinomio.
• aₙ, aₙ₋₁, …, a₁, a₀ son números reales y se llaman coeficientes.

Características de las Funciones Polinómicas

• Ceros: Los valores de x para los cuales f(x) = 0. Estos corresponden a las intersecciones con el eje x.

• Comportamiento: El comportamiento de la gráfica de una función polinómica depende de su grado y del signo del coeficiente principal (aₙ).

Gráficas de Funciones Polinómicas

La forma de la gráfica de una función polinómica depende de su grado. Por ejemplo:

• Grado 1: Línea recta.
• Grado 2: Parábola.
• Grado 3: Curva cúbica.

Esta gráfica, por ejemplo, representa la función polinómica

Cortes con los Ejes

• Corte con el eje y: Se obtiene evaluando la función en x = 0. El punto de corte es (0, a₀).
• Cortes con el eje x: Se obtienen resolviendo la ecuación f(x) = 0.

Aplicaciones de las Funciones Polinómicas

• Modelado de fenómenos: Se utilizan para modelar una gran variedad de fenómenos, como el crecimiento de poblaciones, el movimiento de proyectiles, etc.
• Interpolación: Se utilizan para aproximar funciones más complejas.
• Optimización: Se utilizan para encontrar máximos y mínimos.

Ejemplos y Ejercicios

1. Identificar el grado: f(x) = 3x⁴ – 2x² + 1
2. Encontrar los ceros: f(x) = x³ – 4x
3. Graficar: f(x) = x² – 3x + 2
4. Resolver problemas de aplicación: Modelar la altura de un objeto lanzado al aire en función del tiempo.

Actividades Interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes funciones polinómicas y sus propiedades.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la gráfica de una función polinómica al modificar los coeficientes.

Conclusión

Las funciones polinómicas son una herramienta fundamental en el álgebra y tienen numerosas aplicaciones en diferentes campos. Comprender sus propiedades y cómo graficarlas te permitirá resolver una amplia variedad de problemas.

FUNCIÓN EXPONENCIAL

¿Qué es una Función Exponencial?

Una función exponencial es una función matemática donde la variable independiente (x) aparece como exponente de una base constante (a). Su forma general es:

f(x) = ax

Donde:

• a es un número real positivo y diferente de 1.
• x es la variable independiente.

Características de las Funciones Exponenciales

• Crecimiento o decrecimiento: Si a > 1, la función crece exponencialmente. Si 0 < a < 1, la función decrece exponencialmente.
• Asintota horizontal: La recta y = 0 (eje x) es una asíntota horizontal de la gráfica.

Gráficas de Funciones Exponenciales

La gráfica de una función exponencial tiene una forma característica, similar a una curva que se eleva o se desploma rápidamente.

Cortes con los Ejes

• Corte con el eje y: Se obtiene evaluando la función en x = 0. El punto de corte es (0, 1).
• Corte con el eje x: No hay corte con el eje x, ya que la función exponencial nunca es igual a cero.

Aplicaciones de las Funciones Exponenciales

• Crecimiento poblacional: Modela el crecimiento de poblaciones de bacterias, animales o humanos.
• Desintegración radiactiva: Describe la disminución de la cantidad de un material radiactivo a lo largo del tiempo.
• Interés compuesto: Calcula el valor futuro de una inversión a una tasa de interés compuesta.
• Propagación de enfermedades: Modela la propagación de enfermedades infecciosas.

Ejemplos y Ejercicios

1. Graficar: f(x) = 2^x
2. Resolver: 3^x = 27
3. Aplicaciones: Modelar el crecimiento de una bacteria que se duplica cada hora, si inicialmente hay 100 bacterias.

Actividades Interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes funciones exponenciales y sus propiedades.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la gráfica de una función exponencial al modificar la base.

El Número e y la Función Exponencial Natural

¿Qué es el Número e?

El número e es una constante matemática irracional, aproximadamente igual a 2.71828. Al igual que π, es un número trascendente, lo que significa que no es la raíz de ninguna ecuación polinómica con coeficientes racionales.

¿Por qué es tan importante? Porque aparece de manera natural en muchos problemas matemáticos, físicos y biológicos.

La Función Exponencial Natural

La función exponencial natural es una función exponencial que tiene como base el número e. Se expresa como:

f(x) = ex

¿Por qué es tan especial?

• Tasa de cambio constante: La característica más distintiva de la función exponencial natural es que su tasa de crecimiento en cualquier punto es igual al valor de la función en ese punto. En otras palabras, la pendiente de la tangente a la curva en cualquier punto es igual al valor de la función en ese punto.
• Aplicaciones en cálculo: La función exponencial natural tiene propiedades muy útiles en el cálculo, como ser su propia derivada e integral. Esto la convierte en una herramienta fundamental en el estudio de muchas áreas de las matemáticas.

¿Por qué e es la base más importante?

• Ocurrencia natural: El número e aparece en numerosos contextos, desde el cálculo del interés compuesto continuo hasta la distribución normal en estadística.
• Propiedades únicas: La función exponencial natural tiene propiedades únicas que la hacen especialmente útil para modelar fenómenos de crecimiento y decaimiento.
• Simplificación de cálculos: Al utilizar e como base, muchas fórmulas y cálculos se simplifican considerablemente.

Gráfica de la Función Exponencial Natural

La gráfica de la función f(x) = e^x es una curva creciente que se acerca al eje x pero nunca lo toca.

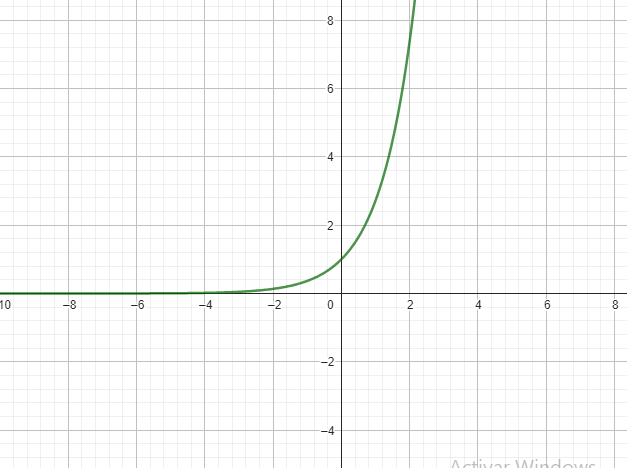
Aplicaciones de la Función Exponencial Natural

• Crecimiento poblacional: Modela poblaciones que crecen a una tasa proporcional a su tamaño.
• Desintegración radiactiva: Describe la disminución de la cantidad de un material radiactivo a lo largo del tiempo.
• Interés compuesto continuo: Calcula el valor futuro de una inversión cuando los intereses se capitalizan continuamente.
• Procesos de enfriamiento y calentamiento: Describe cómo la temperatura de un objeto cambia con el tiempo.
• Muchos otros campos: Física, química, biología, economía, etc.

Ejemplos y Ejercicios

1. Calcular: e² (utilizando una calculadora)
2. Graficar: f(x) = e^-x
3. Resolver: e^2x = 5

Actividades Interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes transformaciones de la función exponencial natural.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la gráfica de la función exponencial natural al modificar los parámetros.

Conclusión

Las funciones exponenciales, el número e y la función exponencial natural son conceptos fundamentales en matemáticas con una amplia gama de aplicaciones. Comprender sus propiedades y cómo utilizarlas te permitirá modelar y analizar una gran variedad de fenómenos en el mundo real.

FUNCIÓN LOGARÍTMICA

¿Qué es una Función Logarítmica?

Una función logarítmica nos indica el exponente al que debemos elevar una base dada para obtener un determinado número. Es decir, nos dice cuántas veces debemos multiplicar la base por sí misma para llegar al resultado.

Una función logarítmica es la inversa de una función exponencial.

Forma general:

y = logₐ(x)

Esto se lee como “y es el logaritmo en base a de x”. Y significa que a elevado a la y es igual a x.

ay = x

Características de las Funciones Logarítmicas

• Asintota vertical: La recta x = 0 (eje y) es una asíntota vertical.
• Crecimiento: Si a > 1, la función es creciente. Si 0 < a < 1, la función es decreciente.

Dado que es imposible obtener un número negativo elevando un número positivo (la base) a cualquier otro, no es posible hablar de logaritmos de números negativos. Por otro lado, dado que no es posible obtener 0 como resultado de elevar un número positivo (la base) a otro, tampoco podemos hablar del logaritmo de 0.

Gráficas de Funciones Logarítmicas

La gráfica de una función logarítmica tiene una forma característica, similar a una curva que crece o decrece lentamente y se acerca al eje y sin tocarlo.

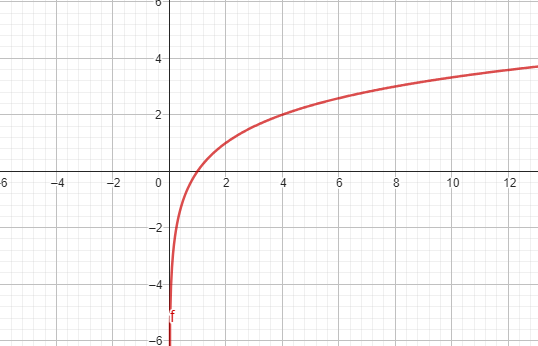
Gráfica de función logarítmica creciente

Cortes con los Ejes

• Corte con el eje y: No hay corte con el eje y, ya que el logaritmo de 0 no está definido.
• Corte con el eje x: Se produce cuando y = 0. En este caso, a⁰ = 1, por lo que el corte con el eje x es en el punto (1, 0).

Aplicaciones de las Funciones Logarítmicas

• Escalas logarítmicas: Se utilizan para representar datos que varían en un rango muy amplio, como la intensidad de los terremotos o el pH.
• Modelos de crecimiento y decaimiento: Se utilizan para modelar fenómenos que crecen o decaen a una tasa proporcional a su tamaño.
• Resolución de ecuaciones exponenciales: Los logaritmos se utilizan para “bajar” los exponentes y resolver ecuaciones.

Ejemplos y Ejercicios

1. Calcular: log₂(8)
2. Graficar: y = log₃(x)
3. Resolver: log₂(x + 1) = 3

Actividades Interactivas

• Software de graficación: Utilizar programas como GeoGebra o Desmos para explorar diferentes funciones logarítmicas y sus propiedades.
• Simulaciones: Realizar simulaciones para visualizar cómo cambia la gráfica de una función logarítmica al modificar la base.

Conclusión

Las funciones logarítmicas son la inversa de las funciones exponenciales y tienen una amplia gama de aplicaciones en la vida real. Comprender sus características y cómo graficarlas te permitirá resolver una gran variedad de problemas.

FUNCIÓN RACIONAL

¿Qué es una Función Racional?

Una función racional es una función que se puede expresar como el cociente de dos polinomios. Es decir, f(x) = p(x) / q(x), donde p(x) y q(x) son polinomios y q(x) ≠ 0.

¿Cómo se Construye una Función Racional?

Para construir una función racional, simplemente tomamos dos polinomios cualesquiera y los dividimos. Por ejemplo:

• f(x) = (x² + 3x – 2) / (x – 1)
• g(x) = 5 / (x² + 4)

En las funciones racionales el denominador no puede ser igual a cero. Los valores que hacen que el denominador se convierta en 0 se llaman asíntotas y se excluyen de la función.

Asíntotas

• Asíntota vertical: Es una línea vertical a la que se acerca la gráfica de la función cuando x se acerca a un valor que no está en el dominio. Generalmente, ocurre cuando el denominador se hace cero.
• Asíntota horizontal: Es una línea horizontal a la que se acerca la gráfica de la función cuando x tiende a infinito o menos infinito.

Cortes con los Ejes

• Corte con el eje y: Se encuentra evaluando la función en x = 0. Si el denominador no es cero en x = 0, entonces la función tiene un corte con el eje y.
• Corte con el eje x: Se encuentran resolviendo la ecuación f(x) = 0, es decir, igualando el numerador a cero y resolviendo para x.

Aplicaciones de las Funciones Racionales

Las funciones racionales tienen una amplia variedad de aplicaciones en la vida real, como:

• Modelado de fenómenos físicos: Por ejemplo, la ley de la gravitación universal.
• Economía: Modelos de oferta y demanda.
• Ingeniería: Diseño de circuitos eléctricos.
• Biología: Modelos de crecimiento poblacional.

Gráficas de Funciones Racionales

Las gráficas de las funciones racionales pueden tener formas muy variadas, dependiendo de los polinomios que la componen. Para graficar una función racional, es útil identificar:

• Dominio y rango.
• Cortes con los ejes.
• Asíntotas.
• Comportamiento de la función en los intervalos determinados por las asíntotas.

Ejemplo

Consideremos la función f(x) = (x+2) / (x-1).

• Dominio: Todos los números reales excepto x = 1.
• Corte con el eje y: Evaluando en x = 0, obtenemos y = -2.
• Corte con el eje x: Resolviendo x + 2 = 0, obtenemos x = -2.
• Asíntota vertical: x = 1.
• Asíntota horizontal: y = 1 (ya que el grado del numerador y del denominador es el mismo).

Actividades para los estudiantes:

• Graficar varias funciones racionales.
• Resolver ecuaciones con funciones racionales.
• Analizar el dominio, rango y asíntotas de diferentes funciones.
• Crear problemas de aplicación utilizando funciones racionales.

Recursos adicionales:

• Libros de texto: Buscar capítulos sobre funciones racionales en libros de texto de matemáticas de segundo de bachillerato.
• Plataformas en línea: Khan Academy, GeoGebra, etc., ofrecen recursos interactivos y videos explicativos.
• Software matemático: Programas como Mathematica o MATLAB permiten graficar y analizar funciones racionales de manera más precisa.

Conclusiones

Las funciones racionales son herramientas poderosas en el mundo de las matemáticas y sus aplicaciones. Nos permiten modelar una amplia variedad de fenómenos reales, desde el movimiento de los planetas hasta el crecimiento de las poblaciones. Su capacidad para describir relaciones inversamente proporcionales y comportamientos asintóticos las hace indispensables en campos como la física, la economía, la ingeniería y las ciencias naturales. Además, su estudio profundiza nuestra comprensión de otros conceptos matemáticos como límites, derivadas e integrales. En resumen, las funciones racionales son una pieza fundamental en el rompecabezas de las matemáticas y nos ayudan a entender mejor el mundo que nos rodea.

FUNCIÓN RADICAL CON ÍNDICE PAR E ÍNDICE IMPAR

¿Qué es una Función Radical?

Una función radical es aquella que involucra una raíz en su expresión. La raíz más común es la raíz cuadrada, pero también podemos encontrar raíces cúbicas, cuartas, etc. De forma general, una función radical se expresa como:

f(x) = ∛a

donde:

• f(x) representa el valor de la función para un valor dado de x.
• ∛ es el símbolo de la raíz, y n es el índice de la raíz.
• a es el radicando, el número al que le estamos sacando la raíz.

Índice Par vs. Índice Impar

El índice de la raíz determina algunas propiedades importantes de la función:

• Índice par: Cuando el índice es par (como en la raíz cuadrada), el radicando debe ser no negativo para que la raíz sea un número real. Esto significa que el dominio de la función estará restringido.
• Índice impar: Cuando el índice es impar (como en la raíz cúbica), el radicando puede ser cualquier número real. El dominio de la función no tendrá restricciones.

Gráficas de Funciones Radicales

La gráfica de una función radical depende del índice y del radicando. En general, las gráficas de las funciones radicales tienen una forma característica, similar a una curva suave que comienza en un punto específico y se extiende hacia el infinito.

Ecuaciones con Radicales

Para resolver ecuaciones con radicales, se suele elevar ambos miembros de la ecuación a la potencia del índice de la raíz. Sin embargo, es importante verificar las soluciones obtenidas, ya que al elevar al cuadrado ambos miembros de una ecuación, pueden aparecer soluciones extrañas.

Cortes con los Ejes

• Corte con el eje y: Se encuentra evaluando la función en x = 0.
• Corte con el eje x: Se encuentra igualando la función a cero y resolviendo la ecuación resultante.

Aplicaciones de las Funciones Radicales

Las funciones radicales tienen numerosas aplicaciones en diversas áreas, como:

• Física: Cálculo de distancias, áreas y volúmenes.
• Geometría: Teorema de Pitágoras, cálculo de áreas de figuras planas.
• Estadística: Cálculo de desviación estándar.

Ejemplos

• Raíz cuadrada: f(x) = √x. Dominio: x ≥ 0. Rango: y ≥ 0.
• Raíz cúbica: f(x) = ∛x. Dominio: todos los números reales. Rango: todos los números reales.

Actividades para los estudiantes

• Graficar diferentes funciones radicales.
• Resolver ecuaciones con radicales.
• Analizar el dominio y rango de funciones radicales.
• Crear problemas de aplicación utilizando funciones radicales.

Recursos adicionales:

• Libros de texto: Buscar capítulos sobre funciones radicales en libros de texto de matemáticas de segundo de bachillerato.
• Plataformas en línea: Khan Academy, GeoGebra, etc., ofrecen recursos interactivos y videos explicativos.
• Software matemático: Programas como Mathematica o MATLAB permiten graficar y analizar funciones radicales de manera más precisa.

Conclusiones

Las funciones radicales son esenciales para comprender y modelar una amplia gama de fenómenos en matemáticas y ciencias. Desde la geometría, donde se utilizan para calcular longitudes y áreas, hasta la física, donde se emplean para describir movimientos y fuerzas, las funciones radicales son una herramienta fundamental. Su estudio nos permite analizar el comportamiento de variables relacionadas de manera no lineal y comprender conceptos clave como dominio, rango y gráficas. En resumen, las funciones radicales son una pieza clave en el rompecabezas matemático y nos ayudan a entender mejor el mundo que nos rodea.