Son relaciones matemáticas que vinculan la medida de un ángulo (expresada en radianes o grados) con las razones entre los lados de un triángulo rectángulo.

Objetivos de la clase:
Recordar las unidades de medida de los ángulos y las definiciones de las relaciones trigonométricas a partir de los cocientes entre los lados de un triángulo rectángulo para analizar las funciones trigonométricas presentadas en el plano cartesiano.
Contenidos:
- Repaso de la medición de ángulos
- Triángulo rectángulo y razones trigonométricas
Actividades:
1. Repaso de la Medición de Ángulos
a) ¿Qué es un ángulo?
- Definición intuitiva: Un ángulo es la abertura formada por dos rayos que comparten un punto en común, llamado vértice.
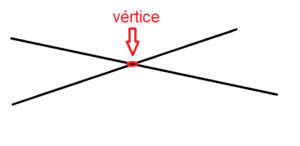
- Representación gráfica:

b) Unidades de medida
- Grados:
- División de una circunferencia en 360 partes iguales.
- Cada parte es un grado (1°).
- Ejemplo: Un ángulo recto mide 90°
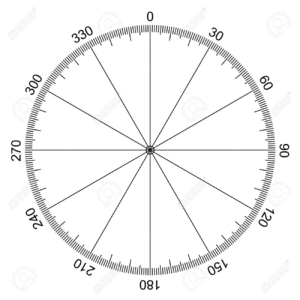
- Radianes:
- Relación entre la longitud de un arco y el radio de una circunferencia.
- Un radián es el ángulo que subtiende un arco de longitud igual al radio.
- Visualización:

- Ventajas de los radianes:
- Son más naturales en muchas fórmulas matemáticas y físicas.
- Simplifican cálculos en cálculo y análisis matemático.
c) Conversión entre grados y radianes
- Fórmulas:

- Ejemplos:

| TABLA DE EQUIVALENCIAS COMUNES | |
| GRADOS | RADIANES |
| 0 | 0 |
| 30 | π/6 |
| 45 | π/4 |
| 60 | π/3 |
| 90 | π/2 |
| 180 | π |
| 270 | 3π/2 |
| 360 | 2π |
2. Triángulo Rectángulo y Razones Trigonométricas
Observa el contenido del siguiente enlace:
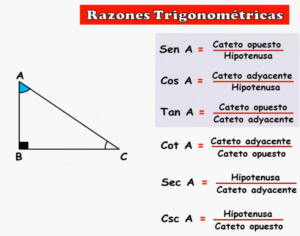
Conclusiones:
Las funciones trigonométricas son importantes en muchas áreas de las matemáticas, la física y la ingeniería. Se utilizan para describir la relación entre los lados y los ángulos de un triángulo rectángulo. También se utilizan para describir la relación entre el tiempo y la posición de un objeto que se mueve en un círculo.
Las funciones trigonométricas se utilizan en muchas aplicaciones prácticas, como la navegación, la astronomía, la ingeniería civil y la ingeniería eléctrica. También se utilizan en muchas áreas de las matemáticas, como el cálculo, el álgebra lineal y la geometría analítica.
