La fuerza como vector, composición y descomposición de fuerzas
La fuerza como vector, composición y descomposición de fuerzas
Objetivos:
- Comprender la naturaleza vectorial de las fuerzas.
- Aprender a representar fuerzas como vectores en un plano.
- Conocer los métodos para componer y descomponer fuerzas.
- Aplicar la descomposición de fuerzas en problemas físicos.
- Explorar aplicaciones prácticas de la composición y descomposición de fuerzas en situaciones del mundo real.
Contenido:
Imagina que estás empujando un coche averiado cuesta arriba, sintiendo cómo cada músculo de tu cuerpo trabaja contra la fuerza de la gravedad. Al mismo tiempo, un amigo te ayuda a empujarlo desde un lado, y te das cuenta de que juntos pueden mover el coche más fácilmente. En este momento, estás experimentando la fuerza como un vector y cómo diferentes fuerzas pueden combinarse para lograr un objetivo común. En esta lección, te sumergirás en el fascinante mundo de las fuerzas, aprendiendo a representar y descomponer fuerzas en sus componentes, y entendiendo cómo estas fuerzas interactúan en el mundo real.
La Fuerza como Vector
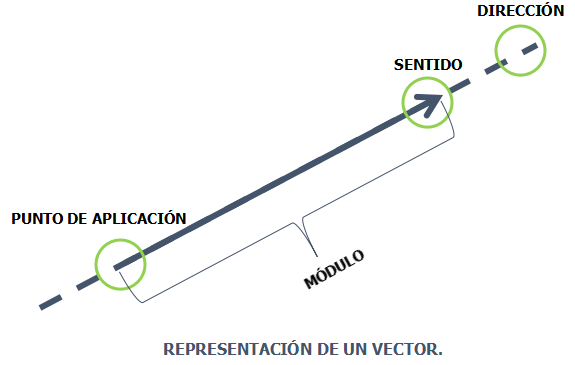
Una fuerza es una interacción que puede cambiar el estado de movimiento de un objeto. Las fuerzas son vectores porque tienen tanto magnitud como dirección. Para representar una fuerza como vector, utilizamos flechas en un plano. La longitud de la flecha indica la magnitud de la fuerza y la dirección de la flecha muestra hacia dónde actúa la fuerza.
Componentes de un Vector
Un vector se puede descomponer en sus componentes perpendiculares, generalmente en las direcciones x (horizontal) e y (vertical). Esto es útil porque facilita la resolución de problemas complejos al tratar con fuerzas en una dimensión a la vez.
- Componentes Rectangulares: Dada una fuerza F con una magnitud F y un ángulo θ respecto al eje x, sus componentes en las direcciones x e y son:
- Fx = F cos(θ)
- Fy = F sin(θ)
- Representación Vectorial: Un vector fuerza F se puede representar como:
- F = Fxi + Fyj de i y j son los vectores unitarios en las direcciones x e y, respectivamente.
Suma de Vectores
Actividades para reforzar lo aprendido
Construcción de un Modelo 3D de Vectores de Fuerza
Objetivo: Visualizar y comprender la composición y descomposición de fuerzas utilizando un modelo físico.
Materiales:
- Palillos o varillas de madera
- Hilo o cuerda fina
- Arcilla de modelar o plastilina
- Regla y transportador
- Marcadores de colores
Instrucciones:

- Preparación de la Base: Usa la arcilla de modelar para crear una base sobre la que montarás tus vectores de fuerza.
- Creación de Vectores: Fija los palillos o varillas de madera en la base, representando vectores de fuerza. Usa el transportador para ajustar los ángulos con precisión.
- Etiquetado: Usa marcadores de diferentes colores para etiquetar cada vector según su magnitud y dirección.
- Composición de Fuerzas: Une varios palillos con hilo para mostrar la composición de fuerzas, colocando la cuerda desde la punta de un vector hasta la cola del siguiente.
- Descomposición de Fuerzas: Usa hilos para descomponer un vector en sus componentes x e y, tirando los hilos horizontal y verticalmente desde la punta del vector.
- Reflexión: Escribe una breve explicación de cómo cada modelo representa la suma o descomposición de fuerzas.
Simulación Interactiva de Vectores de Fuerza
Objetivo: Comprender la composición y descomposición de fuerzas utilizando simulaciones en línea.
Materiales:
- Computadora o tablet con acceso a internet
- Simulador de física (puedes usar PhET Interactive Simulations)
Instrucciones:
- Acceso a la Simulación: Visita el sitio de PhET Interactive Simulations o una plataforma similar y selecciona la simulación “Suma de Vectores.”
- Interacción con la Simulación: Crea diferentes vectores de fuerza ajustando sus magnitudes y direcciones. Experimenta con la suma de vectores y observa la resultante.
- Descomposición de Fuerzas: Usa la simulación para descomponer un vector en sus componentes x e y. Ajusta los ángulos para ver cómo varían las componentes.
- Registro de Resultados: Toma capturas de pantalla de diferentes configuraciones de vectores y anota las conclusiones sobre cómo las fuerzas se componen o descomponen.
- Reflexión: Escribe un breve informe sobre lo que aprendiste acerca de la composición y descomposición de fuerzas a partir de la simulación.
Diseño de un Puente Colgante en Miniatura
Objetivo: Aplicar el concepto de fuerzas vectoriales en el diseño y análisis de estructuras.
Materiales:
- Hilo fuerte o cuerda fina
- Palillos de madera o popotes (pajillas)
- Pegamento fuerte
- Papel, lápiz y regla
- Pesos pequeños para probar el puente
Instrucciones:

- Diseño del Puente: Diseña un puente colgante en miniatura utilizando los materiales proporcionados. Piensa en cómo las fuerzas actuarán sobre los cables y los soportes.
- Construcción: Construye el puente siguiendo tu diseño. Usa hilo o cuerda como cables y palillos para la estructura del puente.
- Análisis de Fuerzas: Dibuja un diagrama de las fuerzas que actúan en diferentes puntos del puente, descomponiendo las fuerzas en sus componentes horizontales y verticales.
- Prueba de Resistencia: Coloca pequeños pesos en el puente para probar su resistencia. Observa cómo se distribuyen las fuerzas y ajusta el diseño si es necesario.
- Informe de Proyecto: Escribe un informe detallando tu diseño, el análisis de fuerzas y los resultados de tus pruebas. Reflexiona sobre cómo los conceptos de fuerzas vectoriales fueron esenciales para el diseño exitoso del puente.
