Conocer matrices es esencial para resolver problemas complejos, organizar datos y modelar situaciones en matemáticas, ciencias, ingeniería y economía.

Objetivos de la clase:
Comprender los conceptos básicos de las matrices, su representación, tipos y operaciones fundamentales como adición y multiplicación.
Contenidos:
- Concepto de matrices y notación
- Igualdad de matrices
- Tipos de matrices (identidad, diagonal, nula, etc.)
- Adición de matrices
- Multiplicación de matrices por un número real
DESARROLLO
Concepto y Representación de las Matrices
Objetivos:
- Definir qué es una matriz.
- Explicar la notación de una matriz y su representación gráfica.
¿Qué es una matriz?
Una matriz es una tabla rectangular de números, símbolos o expresiones dispuestas en filas y columnas. Se utiliza como una herramienta matemática fundamental para organizar y manipular datos de manera estructurada, facilitando el análisis y la resolución de problemas en diversas áreas como:
- Sistemas de ecuaciones lineales: Permiten resolver múltiples ecuaciones simultáneamente.
- Ciencias de la computación: Se aplican en programación, gráficos por computadora y procesamiento de imágenes.
- Economía y finanzas: Sirven para modelar y analizar datos de inventarios, costos y proyecciones.
- Física e ingeniería: Ayudan en la representación de vectores, transformaciones y simulaciones
Su representación es u n arreglo rectangular de números dispuestos en filas y columnas
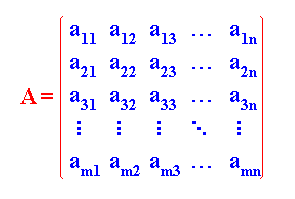
La notación estándar de matrices es:
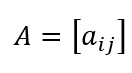
Dónde: aij representa el elemento en la i-ésima fila y la j-ésima columna
Cada elemento de una matriz pertenece al conjunto de los números reales.
Las dimensiones de una matriz indican el número de filas y columnas de la matriz en ese orden. Una matriz que tenga 2 filas (horizontales) y 3 columnos sería una matriz 2×3
Ejemplos:
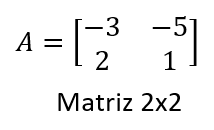
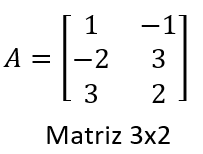
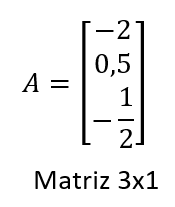
Exploración interactiva
- Actividad TIC: Utiliza Matrix Calc o una herramienta similar para mostrar cómo se representa una matriz en línea. Crea y explora matrices de diferentes dimensiones
- Actividad de investigación: ¿En qué situaciones prácticas se utilizan matrices en la vida diaria?
Reflexión personal
- ¿Por qué es importante conocer la notación y representación de matrices?
Actividad individual:
- Crea 5 matrices de diferentes tamaños en Matrix Calc y anotar los elementos en tu cuaderno
Igualdad de Matrices
Objetivos:
- Definir y explicar qué significa la igualdad de matrices.
- Enseñar cómo comparar dos matrices para determinar si son iguales.
¿Qué representa la igualdad de matrices?
Dos matrices se consideran iguales si tienen el mismo número de filas y columnas y sus elementos correspondientes son iguales
En símbolos A=[aij] y B=[bij] son iguales si tienen el mismo número de filas y columnas y sus elementos correspondientes aij=bij para todo i, j
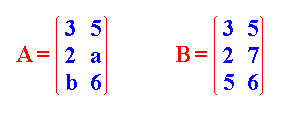
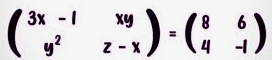
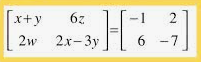
Exploración interactiva
- Actividad TIC: Usa Matrix Calc para verificar si dos matrices dadas son iguales.
Reflexión personal
- Reflexionar sobre la importancia de la igualdad de matrices en operaciones más avanzadas
Actividad individual:
- En cada par de matrices dadas en los ejercicios del 1 al 5, comparar si son iguales o diferentes y justificar sus respuestas
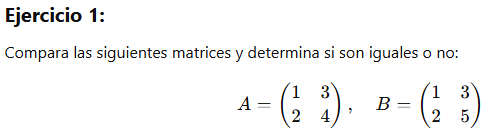



Tipos de Matrices
Objetivos:
- Identificar y clasificar diferentes tipos de matrices (identidad, diagonal, nula, etc.).
- Aprender las propiedades de cada tipo de matriz.
¿Qué tipos de matrices existen?






Para reforzar este contenido, puedes ver este video:
Tareas:
- Crea ejemplos de matrices identidad, nula y diagonal en Matrix Calc. Copia en tu cuaderno
- Realiza la clasificación de matrices en las actividade de los siguientes enlaces:
https://www.liveworksheets.com/es/w/es/matematicas-ciencias-sociales/2126851
https://www.liveworksheets.com/w/es/matematicas/438585
Suma de Matrices
La suma de matrices es una operación matemática que permite combinar matrices del mismo tamaño, sumando sus elementos correspondientes.
Objetivos:
- Comprender el concepto y las condiciones para sumar matrices.
- Aplicar la suma de matrices en ejercicios prácticos.
- Resolver problemas usando la propiedad de la conmutatividad y la asociatividad.
¿Cómo sumamos matrices?
¿Qué es la suma de matrices?
La suma de matrices es una operación en la que se suman los elementos correspondientes de dos matrices que tienen las mismas dimensiones. Si las matrices tienen diferente tamaño, no se pueden sumar.
Condiciones para sumar matrices:
- Las matrices deben ser del mismo tamaño. Es decir, deben tener el mismo número de filas y el mismo número de columnas.
- Si tenemos dos matrices A y B, con dimensiones m x n, entonces la matriz resultante C = A + B será tambíen de dimensiones m x n.
Proceso paso a paso:
- Asegúrate de que ambas matrices tengan las mismas dimensiones.
- Suma los elementos correspondientes de cada matriz. Por ejemplo, si

la suma será

Propiedades de la suma de matrices:
- Conmutatividad: A+B = B+A
- Asociatividad: (A + B) + C = A + (B + C)
- Existencia de matriz nula: Existe una matriz cero (matriz cuyos elementos son todos cero) que no altera la suma: A + 0 = A
Ejercicios modelo:



Tarea de clase:
Realiza las actividades que se presentan en los enlaces:
https://www.liveworksheets.com/es/w/es/matematicas/1348249
https://www.liveworksheets.com/es/w/es/matematicas/884005
Multiplicación de matrices por un número real (escalar)
La multiplicación de matrices por un escalar consiste en multiplicar cada elemento de una matriz por un número real dado.
Objetivos:
- Comprender el concepto y las condiciones para multiplicar matrices por un escalar.
- Aplicar la multiplicación por escalar en ejercicios prácticos.
- Relacionar la multiplicación por escalar con aplicaciones prácticas, como en transformaciones matemáticas.
¿Qué es la multiplicación por un escalar?
La multiplicación por un escalar es una operación que se realiza cuando una matriz se multiplica por un número real (llamado escalar). Al realizar esta operación, cada elemento de la matriz se multiplica por el escalar, generando una nueva matriz.
Condiciones para multiplicar una matriz por un escalar:
- No hay restricciones en las dimensiones de la matriz.
- El escalar puede ser cualquier número real (positivo, negativo, fracción, o decimal).
Proceso paso a paso:


Ejemplos de aplicación de la multiplicación de una matriz por un escalar en diferentes ámbitos:


Ejercicios modelo:




Tarea de clase:
Realizar las tareas que se presentan en los enlaces:
https://www.liveworksheets.com/es/w/es/matematicas/1015905
Conclusiones:
¡Bien hecho! En este tema has trabajado bastante acerca de matrices, y aquí va un resumen de lo que ya deberías manejar:
- Concepto y notación de matrices:
Ahora sabes que una matriz es básicamente una tabla de números organizada en filas y columnas. Aprendiste a identificar su tamaño (m×n) y a ubicar elementos específicos usando subíndices. - Igualdad de matrices:
Ya puedes identificar cuándo dos matrices son iguales: tienen que ser del mismo tamaño y todos sus elementos correspondientes tienen que ser iguales. - Tipos de matrices:
Conoces los diferentes tipos de matrices y para qué sirven:- Las matrices fila y columna, que como su nombre lo indica sólo tienen una fila o una columna con sus respectivos elementos
- La matriz identidad (es como el “1” de las matrices en multiplicación).
- La matriz diagonal (solo tiene números fuera del cero en la diagonal principal).
- La matriz nula (todos sus elementos son cero).
- La matriz cuadrada (tiene el mismo número de filas y columnas, y es muy importante para operaciones más avanzadas).
- Suma de matrices:
Entendiste cómo sumar matrices elemento a elemento y que sólo se pueden sumar si tienen las mismas dimensiones. Además, sabes que el orden no importa al sumar (conmutatividad) y puedes agrupar sumas como quieras (asociatividad). - Multiplicación de matrices por un número real:
Ahora puedes multiplicar una matriz por un escalar, aplicando la operación a cada elemento. También vimos que esta operación tiene propiedades útiles, como la distributiva, y algunos ejemplos prácticos donde se usa, como en gráficos, presupuestos o transformaciones.
En resumen: Has aprendido los fundamentos de las matrices, que son súper importantes para resolver problemas más complejos y para muchas aplicaciones prácticas. ¡Sigue así, que estás construyendo una base sólida para el futuro! En el siguiente tema vas a aprender multiplicación de matrices.
