La relación entre límites laterales determina si el límite global existe; los límites infinitos describen funciones que tienden a infinito.
Objetivos de la clase:
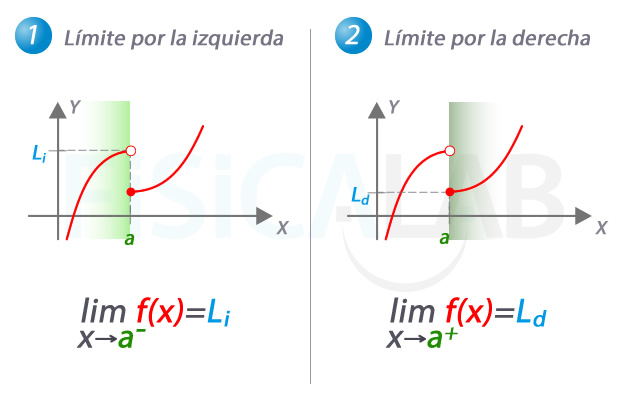
-Comprender qué son los límites laterales finitos.
-Aprender a calcular los límites laterales de una función en un punto.
-Diferenciar entre límite lateral izquierdo y derecho.
Contenidos:
Observemos el siguiente video:
Luego de ver el video, vamos a trabajar las principales ideas presentadas.
Al finalizar, debemos realizar las dos actividades planteadas en el cuaderno de materia
https://gamma.app/docs/Limites-Laterales-Finitos-y-su-Relacion-con-los-Limites-Globales-3y5i9pdbdkpwney
Actividad 1: Juego de Detectives de Límites
- Descripción:
- Divide a la clase en grupos de 3-4 estudiantes.
- Reparte tarjetas con diferentes funciones y puntos donde deben calcular los límites laterales.
- Cada grupo debe investigar y encontrar los límites laterales izquierdo y derecho en el punto indicado.
- Ejemplo de función para la tarjeta: f(x)={3x+2si x<14x−1si x≥1f(x) = \begin{cases} 3x + 2 & \text{si } x < 1 \\ 4x – 1 & \text{si } x \geq 1 \end{cases}f(x)={3x+24x−1si x<1si x≥1
- Los estudiantes deben calcular: limx→1−f(x)ylimx→1+f(x)\lim_{x \to 1^-} f(x) \quad \text{y} \quad \lim_{x \to 1^+} f(x)x→1−limf(x)yx→1+limf(x)
- Después de 5 minutos, cada grupo presenta sus resultados. Se premia al grupo que lo resuelva correctamente y explique bien el proceso.
- Duración: 10 minutos.
Actividad 2: Carrera de Gráficos y Límites
- Descripción:
- Los estudiantes dibujan la gráfica de una función dada en la pizarra o en una hoja de papel.
- Luego, deben marcar y calcular los límites laterales en puntos específicos.
- Función a graficar: f(x)=∣x−2∣x−2f(x) = \frac{|x – 2|}{x – 2}f(x)=x−2∣x−2∣
- Puntos a analizar: x=2x = 2x=2.
- Los estudiantes deben identificar y calcular: limx→2−f(x)ylimx→2+f(x)\lim_{x \to 2^-} f(x) \quad \text{y} \quad \lim_{x \to 2^+} f(x)x→2−limf(x)yx→2+limf(x)
- Discuten en sus grupos cómo cambia la función a medida que se acercan a x=2x = 2x=2 desde ambos lados.
- El primer grupo en completar la tarea con la gráfica correcta y la explicación detallada gana.
Conclusiones:
Cálculo de Límites Laterales: Los estudiantes aprenden a calcular límites laterales y entienden su significado.
Relación con Límite Global: El límite global existe solo si los límites laterales coinciden.
Aplicación Práctica: Los límites laterales tienen relevancia en situaciones reales como la velocidad de un vehículo al frenar.
