
¡Vamos a sumergirnos en el mundo de las matemáticas con un enfoque emocionante! El método de igualación es como resolver un rompecabezas donde tienes que emparejar las piezas correctas. Imagina que tienes dos ecuaciones y quieres encontrar el valor de las incógnitas. Con el método de igualación, buscamos que una de las incógnitas sea la misma en ambas ecuaciones. Luego, igualamos las ecuaciones y resolvemos para descubrir el valor de cada incógnita.
¡Es sencillo y poderoso! Prepárate para convertirte en un maestro de la resolución de sistemas de ecuaciones lineales usando igualación. 📘✨
¿Te gustaría saber más sobre los pasos a seguir?
¿Listo para empezar?
Learning Goals
- Comprender el método de igualación: Aprender cómo y por qué funciona el método de igualación para resolver sistemas de ecuaciones lineales.
- Identificar las incógnitas: Reconocer las incógnitas en el sistema de ecuaciones y saber cómo trabajar con ellas.
- Aplicar transformaciones: Saber cómo modificar las ecuaciones para igualar una de las incógnitas.
- Resolver ecuaciones simplificadas: Ser capaz de igualar y resolver las ecuaciones resultantes para encontrar los valores de las incógnitas.
CONTENIDO
Reglas
Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.
Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.
Para el Método de Reducción, procederemos así:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones.
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación.
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda.
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita.
Ejemplo:
Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.
Sistema:
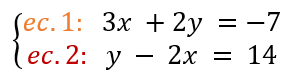
Seguimos las reglas:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones. Para nuestro ejemplo, vamos a despejar “y” de ambas ecuaciones:
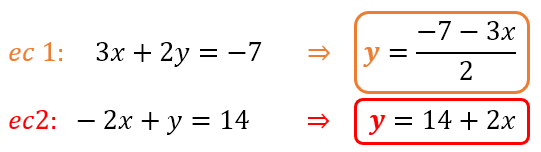
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación. Como despejamos “y” de ambas ecuaciones, y dado que “y=y”, reemplazamos los valores de esta en una nueva ecuación (ec. 3):
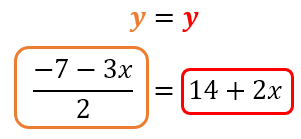
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda, que en este caso, es “x”.
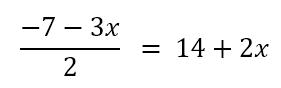
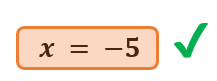
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita. En nuestro caso, podemos sustituirlas incluso en cualquiera de las dos ecuaciones despejadas anteriormente. Por facilidad, escojamos reemplazar el valor de x=-5 en la ecuación que anteriormente encerramos en rojo:
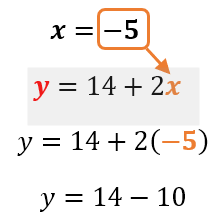

¡Y listo!
Podemos presentar la solución como un conjunto:
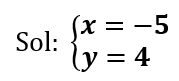
Ejercicios propuestos:
Solucionar los siguientes sistemas de ecuaciones por el método de igualación.
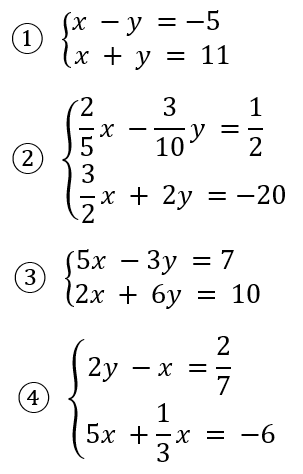
Soluciones:
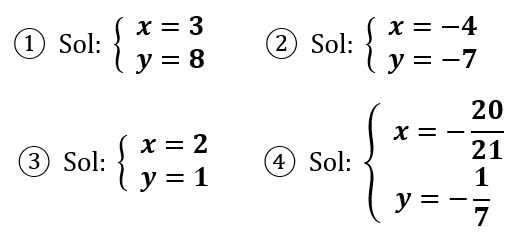
Aplicaciones

Gestión de Recursos Humanos: En una empresa, los gerentes pueden utilizar el método de igualación para asignar empleados a diferentes proyectos. Al igualar las necesidades de habilidades con las capacidades de los empleados, se optimiza la asignación de recursos humanos.
Solución de Problemas de Mezclas: En la industria alimentaria o química, se pueden usar sistemas de ecuaciones lineales para encontrar las proporciones adecuadas de ingredientes en una mezcla. El método de igualación permite determinar estas proporciones de manera precisa.
Planificación Financiera: Los asesores financieros pueden usar el método de igualación para equilibrar ingresos y gastos en la planificación presupuestaria. Esto ayuda a garantizar que las diferentes fuentes de ingresos cubran todas las categorías de gastos.
