
Las ecuaciones de segundo grado con una incógnita son como acertijos matemáticos que nos permiten encontrar soluciones a problemas cotidianos de manera eficiente y precisa. Estas ecuaciones, que se presentan en la forma ax2 + bx + c = 0, nos abren la puerta a un mundo lleno de curvas parabólicas y soluciones fascinantes. ¡Prepárate para desentrañar los misterios detrás de estas elegantes ecuaciones y descubre cómo resolverlas te empoderará en el mundo de las matemáticas y más allá! 🧩📐✨.
Learning Goals
- Identificar la ecuación: Reconocer y escribir ecuaciones de segundo grado en su forma estándar ax2+bx+c = 0.
- Métodos de resolución: Aprender y aplicar el método de factorización para resolver las ecuaciones.
- Discriminante: Entender el papel del discriminante b2 – 4ac y cómo determina la naturaleza de las soluciones (reales y distintas, reales e iguales, o complejas).
- Soluciones de la ecuación: Determinar las soluciones (raíces) de la ecuación y cómo se relacionan con los coeficientes de la ecuación cuadrática.
- Verificar las soluciones: Comprobar la exactitud de las soluciones obtenidas al sustituirlas en la ecuación original.
CONTENIDO
Indicaciones y recomendaciones generales:
- Iguala toda la ecuación a cero (0), pasando todos los términos a un solo lado, respetando las reglas del despeje de ecuaciones.
- Ordena la ecuación.
- Evita las fracciones. Pon la ecuación en enteros.
Nota: a las soluciones también se las conoce como ceros o raíces.
Resolución por casos de factorización
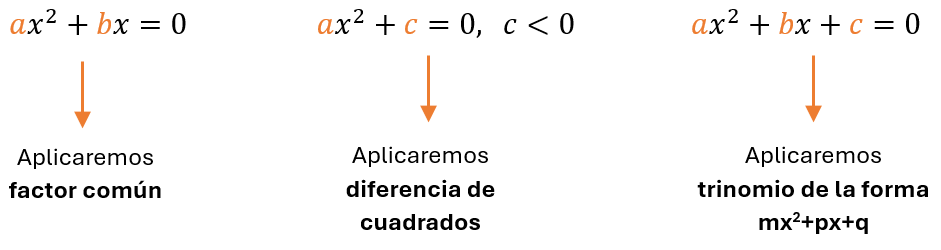
Por facilidad, utilizaremos únicamente tres casos de factorización:
- Factor común
- Diferencia de cuadrados o simple despeje
- Trinomio de la forma mx2+px+q
Factor común:
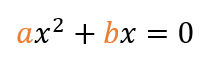
El factor común de este caso es “x”. La expresión quedaría separa por dos factores: el primero sería x, y el segundo sería un paréntesis que encierra a la expresión ax+b. Finalmente, estarían igualadas a cero. Luego, se igualan ambos factores con cero, y se despejan, obteniendo dos soluciones, una por cada factor. Así:
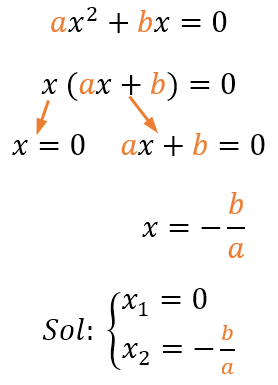
Ejemplos:
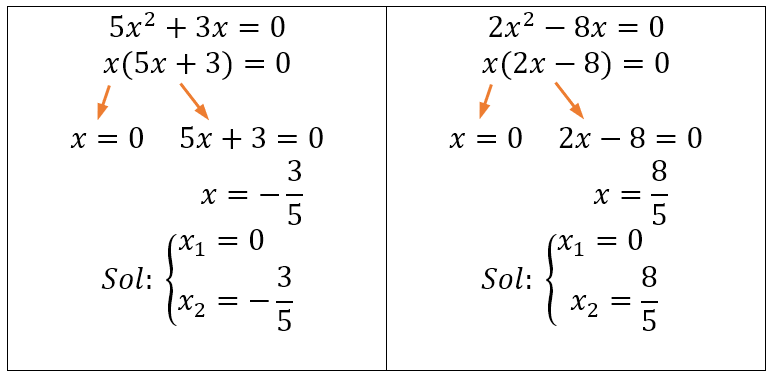
Diferencia de cuadrados o simple despeje:
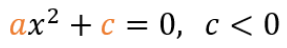
Para que pueda operarse como diferencia de cuadrados, es necesario que los coeficientes a y c sean de signos opuestos. Sin embargo, no siempre se da este caso. Por ello, resulta mejor el simple despeje para este caso. Sin embargo, es necesario aclarar que, al momento de pasar el cuadrado como raíz al otro lado, se generan dos respuestas iguales pero de signo contrario. Así:
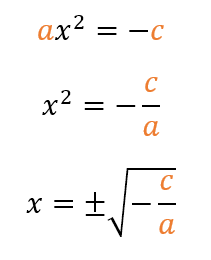
Ejemplos:
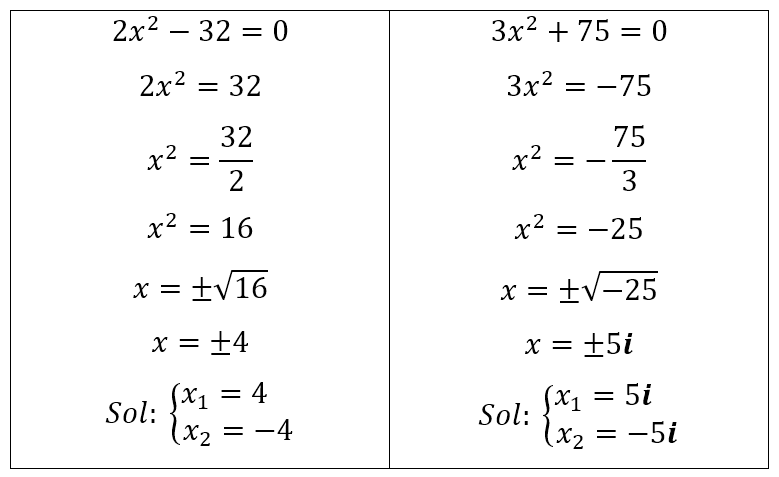
Trinomio de la forma mx2+px+q:
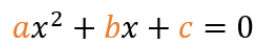
Para este caso en el que se encuentran presentes todos los coeficientes, haremos el siguiente procedimiento general:
- Asegurar que el coeficiente a sea positivo.
- Multiplicamos el coeficiente a por el coeficiente c, y ese será el nuevo valor de c.
- Abrimos dos paréntesis y en cada uno pondremos un binomio. El primer término de cada binomio es ax, el signo que la mitad del primer paréntesis es el mismo de b, y el signo del segundo paréntesis es una ley de signos entre b y c.
- Para completar cada binomio, debemos buscar dos números, de tal forma que: si los signos de cada paréntesis son iguales, entonces estos dos números sumados den b; pero si los signos son opuestos, entonces estos dos números restados den el número den b. Además, esos números, multiplicándose, deben dar el valor de c. El número de mayor peso se coloca en el primer paréntesis, y el de menor peso en el segundo paréntesis.
- Igualamos cada binomio a cero, y despejamos la incógnita.
Expliquémoslo mejor con un ejemplo.
Ejemplos:
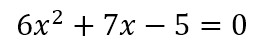
Asegurar que el coeficiente a sea positivo. En el caso de nuestro ejemplo, a=6 es positivo.
Multiplicamos el coeficiente a=6 por el coeficiente c=5 (no tomamos en cuenta el signo), y ese será el nuevo valor de c=30.
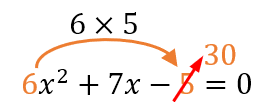
Abrimos dos paréntesis y en cada uno pondremos un binomio. El primer término de cada binomio es ax (es decir, 6x en nuestro ejemplo), el signo que la mitad del primer paréntesis es el mismo de b (positivo en nuestro ejemplo), y el signo del segundo paréntesis es una ley de signos entre b y c (+ y – da –).
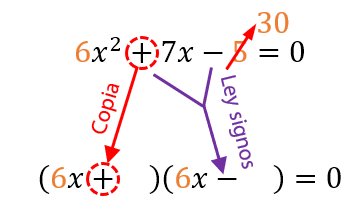
Para completar cada binomio, debemos buscar dos números, y dado que los signos de los paréntesis son opuestos, estos dos números restados den el número den b=7. Además, esos números, multiplicándose, deben dar el valor de c=30.
Los dos números que restados dan 7 y multiplicados 30. Los números son 10 y 3, puesto que 10-3=7, y 10×3=30. El de mayor peso es 10 (va en el primer paréntesis), y el de menor peso es 3 (va en el segundo).
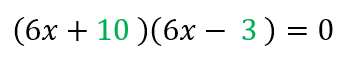
Igualamos cada binomio a cero, y despejamos la incógnita.
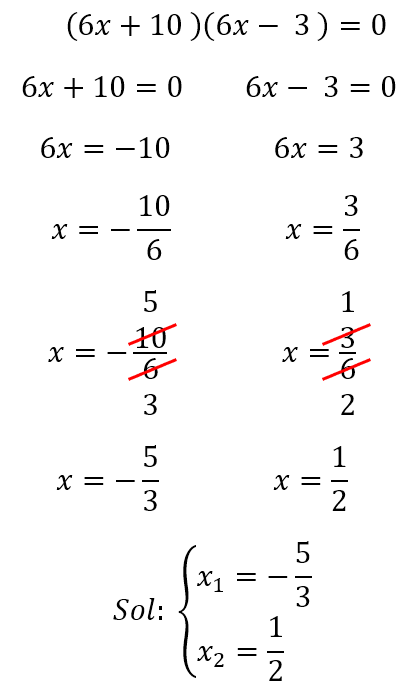
Naturaleza de las raíces
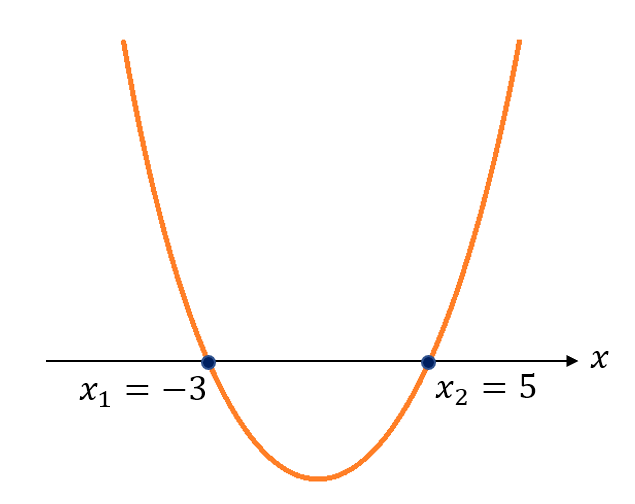
- 2 raíces reales desiguales: cuando el valor de x1 y x2 son diferentes. En la gráfica, las raíces cortan al eje “x” en dos valores. Por ejemplo, si las raíces resultantes de la resolución de la ecuación cuadrática fueran x1=-3 y x2=5, la gráfica podría ser:
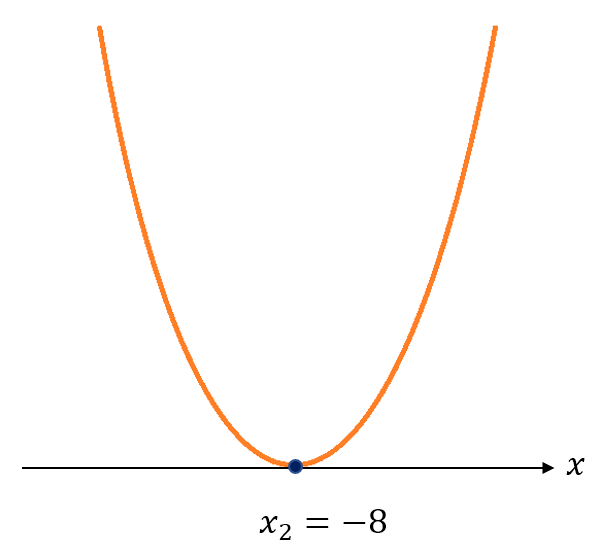
- 1 raíz real: dado que las dos soluciones o raíces son exactamente iguales, se toma en cuenta como si fuera una sola raíz. En la gráfica, esta raíz pasa “topando” al eje “x” en un solo punto, y se regresa. Por ejemplo, si las raíces resultantes de la resolución de la ecuación cuadrática fueran x1=-8 y x2=-8, entonces se toman como una sola raíz, x=-8, y la gráfica sería, por ejemplo:
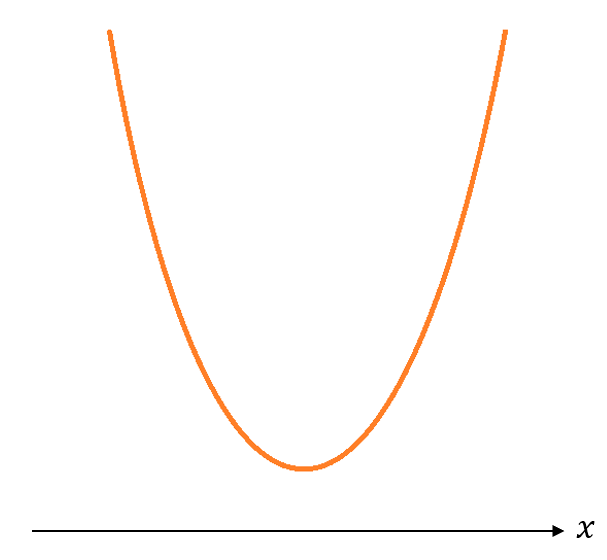
- 2 raíces complejas conjugadas: Estas raíces tienen una parte real y una parte imaginaria. Esa combinación hace que estos números se llamen complejos. Debido a que son iguales, y solo cambia el signo de la parte imaginaria, se llaman conjugados. Debido a su naturaleza de raíces complejas, no pueden ser graficadas, por lo que la parábola no atraviesa ni topa al eje “x” en ningún punto, sino que está distanciada del eje “x”. Por ejemplo, si las raíces resultantes de la resolución de la ecuación cuadrática fueran x1=5-2i y x2=5+2i, la gráfica podría ser:
Naturaleza de las raíces identificadas por el DISCRIMINANTE
El discriminante es un número que se obtiene de operar con los coeficientes (a, b y c) de la ecuación cuadrática siguiendo la siguiente fórmula, para determinar si la ecuación tiene 2 raíces reales, 1 raíz real o 2 raíces complejas conjugadas, sin necesidad de calcular las raíces. La fórmula del discriminante es:
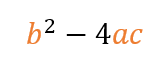
- Si el número resultante es positivo (es decir, mayor que cero), entonces la ecuación tiene 2 raíces reales desiguales.
- Si el número resultante es cero, entonces la ecuación tiene 1 raíz real (o, dicho de otro modo, 2 raíces reales iguales que, al ser iguales, se consideran como una única raíz real).
- Si el número resultante es negativo (es decir, menor que cero), entonces la ecuación tiene 2 raíces complejas conjugadas.
Aplicaciones

Trayectoria de un Proyectil: Para calcular la altura y distancia que un objeto lanzado alcanzará, como una pelota de béisbol. La fórmula de la trayectoria incluye una ecuación cuadrática.
Optimización de Áreas: Para encontrar el tamaño máximo o mínimo de una parcela de tierra dada una cierta cantidad de material para el cercado, como en la agricultura o construcción.
Economía y Finanzas: Para determinar el punto de equilibrio en costos y beneficios. Por ejemplo, calcular el número de productos que deben venderse para cubrir costos y obtener ganancias.
