
La fórmula general para resolver ecuaciones cuadráticas es como una llave maestra en el mundo de las matemáticas. Imagina que tienes una ecuación en la forma ax2+bx+c=0, donde a, b y c son números. La fórmula general te permite encontrar las soluciones (o raíces) de esta ecuación de manera fácil y rápida.
Esta fórmula es poderosa porque puede resolver cualquier ecuación cuadrática, sin importar los valores de a, b y c. Es una herramienta fundamental para estudiantes y profesionales, ya que aparece en diversas áreas como la física, la ingeniería y la economía. ¡Una vez que la domines, estarás listo para enfrentar cualquier desafío cuadrático! 📘✨
Learning Goals
- Identificar Componentes: Aprenderás a reconocer los elementos clave de una ecuación cuadrática.
- Resolver Problemas: Serás capaz de solucionar ecuaciones cuadráticas de manera eficiente.
- Determinar Soluciones: Entenderás cómo saber cuántas soluciones tiene una ecuación cuadrática y de qué tipo son.
- Aplicar en la Vida Real: Utilizarás ecuaciones cuadráticas para resolver problemas prácticos en situaciones cotidianas.
- Mejorar Habilidades: Desarrollarás tus habilidades matemáticas generales al trabajar con ecuaciones cuadráticas.
CONTENIDO
Identificando los coeficientes:
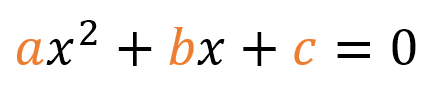
- a Coeficiente principal: es el que multiplica con x2. Debe estar presente.
- b Coeficiente secundario: es el que multiplica con x. Este puede o no estar presente.
- c Ordenada al origen: es el último término, va solo y no multiplica con x. Este puede o no estar presente.
Nota 1: Los coeficientes deben tomarse con todo y su signo.
Nota 2: Los términos que no existen, tienen como coeficiente el cero. Los términos medio y final, correspondientes a b y c pueden estar ausentes y valer cero, pero el coeficiente a no puede faltar en la ecuación cuadrática.
Ejemplo 1:
En la ecuación cuadrática:
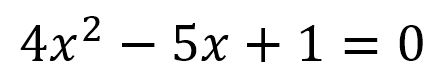
Los coeficientes son:
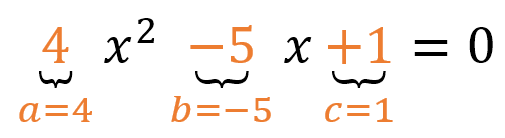
Ejemplo 2:
En la ecuación cuadrática:
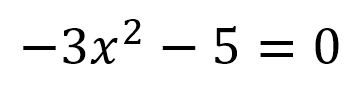
Los coeficientes son:
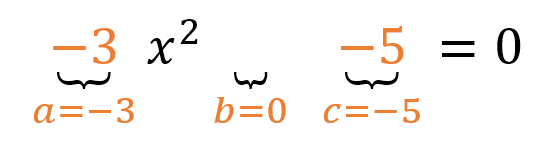
b vale cero debido a que el término de la mitad no existe en el ejercicio planteado.
Ejemplo 3:
En la ecuación cuadrática:
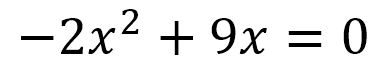
Los coeficientes son:
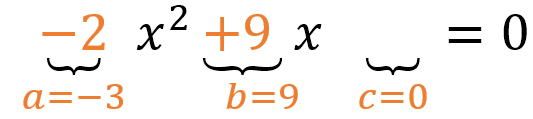
c vale cero debido a que el término final no existe en el ejercicio planteado.
Fórmula general:
La fórmula general nos permite hallar las raíces (también llamadas soluciones o ceros) de la ecuación cuadrática, independientemente de cómo esté presentada, de los coeficientes presentes o ausentes, del caso de factorización, etc.
Una sola fórmula para todos los casos.
Con ella podemos determinar 2 raíces reales, 1 raíz real o 2 raíces complejas conjugadas, dependiendo de la ecuación.
La fórmula general para resolver ecuaciones cuadráticas es:
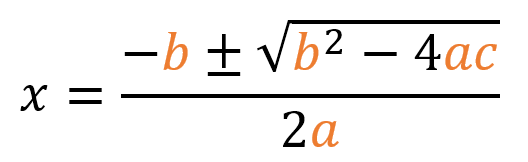
Ejemplo 1:
Para siguiente ecuación cuadrática:
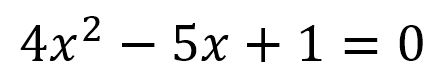
Calcula sus raíces.
- Determinamos primero sus coeficientes:
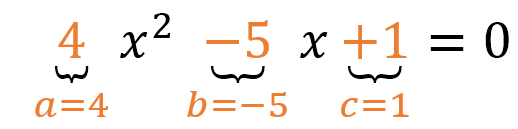
- Reemplazamos los coeficientes en la fórmula general:
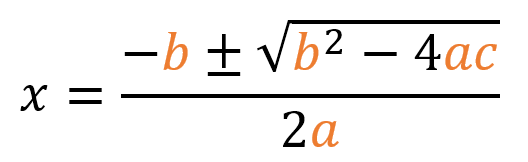
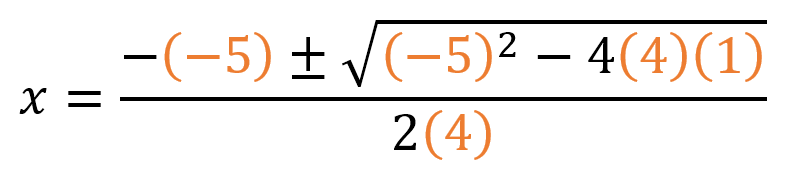
- Resolvemos:
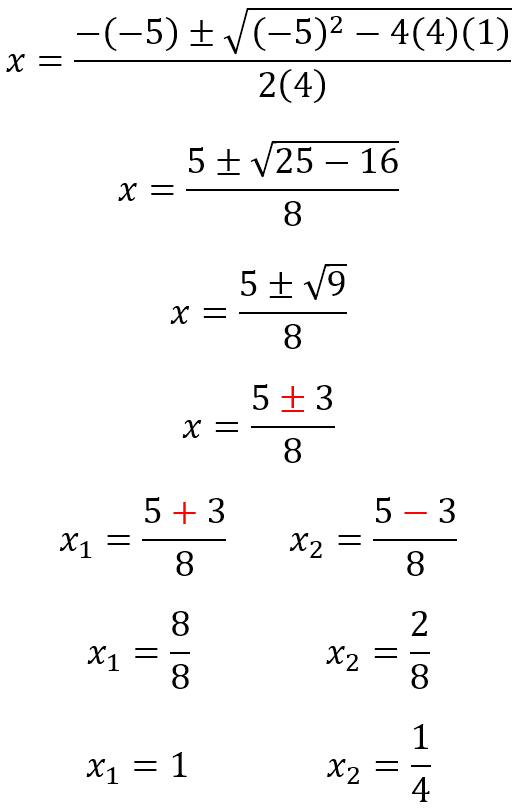
Las raíces o soluciones de la ecuación son:

Son dos raíces reales diferentes.
Ejemplo 2:
Para siguiente ecuación cuadrática:
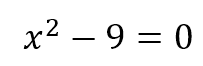
Calcula sus raíces.
- Determinamos primero sus coeficientes:
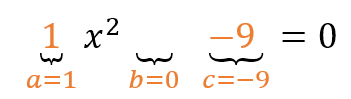
- Reemplazamos los coeficientes en la fórmula general:
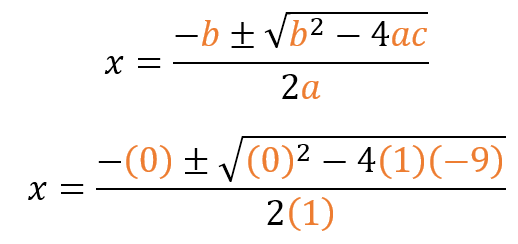
- Resolvemos:
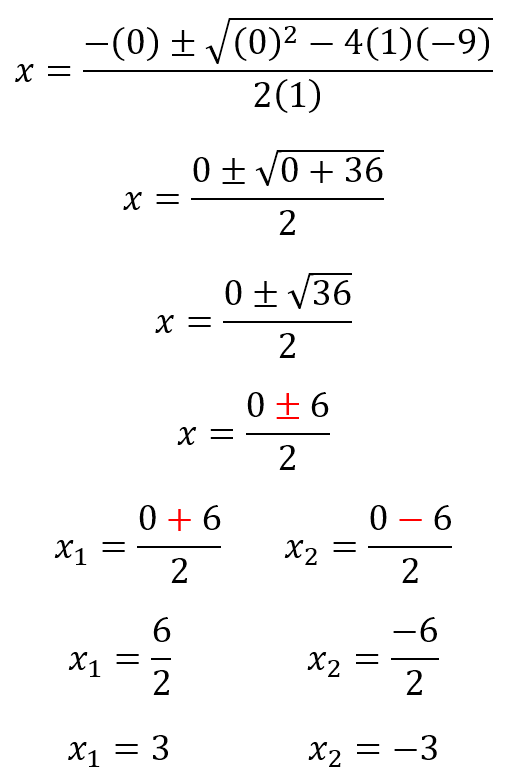
Las raíces o soluciones de la ecuación son:

Son dos raíces reales diferentes.
Ejemplo 3:
Para siguiente ecuación cuadrática:
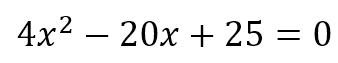
Calcula sus raíces.
- Determinamos primero sus coeficientes:
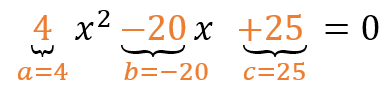
- Reemplazamos los coeficientes en la fórmula general:
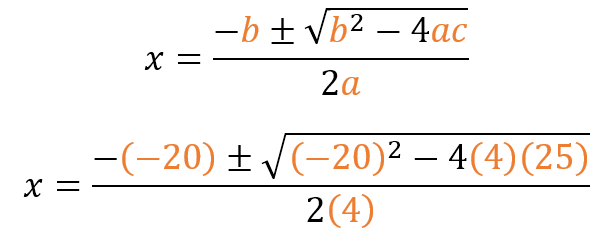
- Resolvemos:
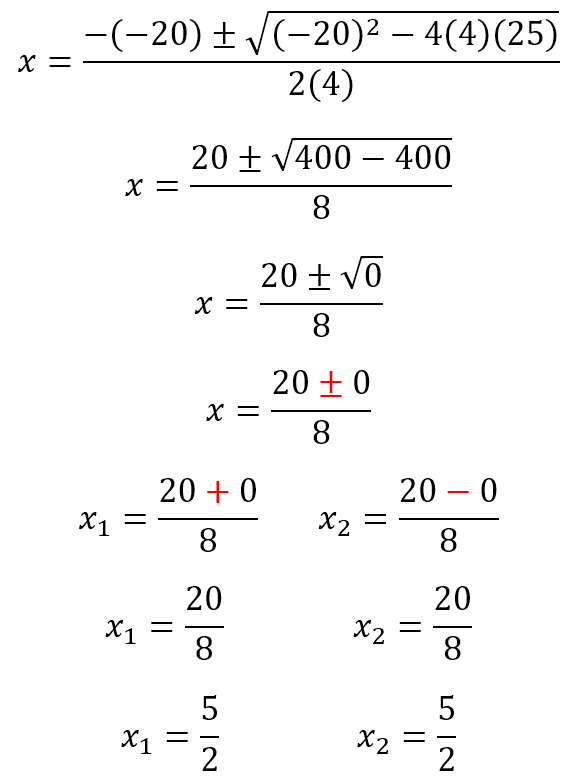
Dado de las raíces son las mismas, podemos decir que tiene 1 raíz real:
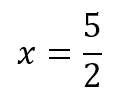
Aplicaciones

Control de Gastos Personales:
- Con gráficas de barras o histogramas, puedes visualizar la distribución de tus gastos mensuales por categorías (alimentación, transporte, entretenimiento, etc.). Esto te ayuda a identificar en qué áreas estás gastando más y ajustar tu presupuesto de manera efectiva.
Seguimiento de Actividad Física:
- Las aplicaciones de actividad física y salud suelen utilizar gráficos de barras y pictogramas para mostrar la cantidad de pasos diarios, calorías quemadas o minutos activos en la semana. Esto permite ver el progreso y ajustar rutinas según los objetivos de actividad.
Distribución de Tiempos de Tráfico:
- Los histogramas se utilizan para analizar el tiempo promedio de tráfico en ciertos horarios. Por ejemplo, en una ciudad, puedes ver en qué momentos del día el tráfico es más intenso y planificar tus trayectos para evitar los picos de congestión.
Encuestas de Satisfacción del Cliente:
- Los gráficos de barras son útiles para presentar los resultados de encuestas, como la satisfacción de clientes en una tienda. Esto facilita visualizar la opinión general sobre diferentes aspectos del servicio y ayuda a realizar mejoras específicas.
Monitoreo del Rendimiento Académico:
- Los profesores pueden usar gráficas de barras o pictogramas para mostrar el rendimiento de los estudiantes en diferentes áreas (exámenes, tareas, participación). Esto ayuda tanto a los docentes como a los estudiantes a identificar fortalezas y áreas de mejora en el aprendizaje.
