Medidas de ángulo: sexagesimales, radianes, centesimales. Conversión de ángulos.

Los ángulos están presentes en nuestra vida cotidiana de maneras que a menudo pasamos por alto. Desde la arquitectura de nuestros edificios hasta la forma en que giramos el volante de un coche, los ángulos son fundamentales para el mundo que nos rodea. Sin embargo, la manera en que medimos estos ángulos puede variar dependiendo de la aplicación y el contexto. En esta unidad, exploraremos las tres principales formas de medir ángulos: sexagesimales, radianes y centesimales. Cada una de estas medidas tiene sus propias características y usos. Además, aprenderemos a convertir ángulos entre estas diferentes unidades, una habilidad esencial para resolver problemas en matemáticas, física e ingeniería.

Importancia de las Medidas de Ángulos
Comprender y trabajar con diferentes medidas de ángulos nos permite:
- Resolver problemas geométricos y trigonométricos con mayor precisión.
- Aplicar conceptos matemáticos en disciplinas como la física, la ingeniería y la arquitectura.
- Mejorar nuestras habilidades de pensamiento crítico y analítico al manejar diferentes sistemas de medida.
¡Prepárate para una fascinante exploración del mundo de los ángulos y descubre cómo estas medidas se aplican en el mundo real y en el ámbito académico!
Learning Goals
- Comprender las diferentes unidades de medida de ángulos: Serás capaz de explicar las diferencias entre los sistemas sexagesimal, de radianes y centesimal, y en qué contextos se utilizan cada uno.
- Calcular ángulos en distintos sistemas: Aprenderás a calcular ángulos en grados sexagesimales, radianes y grados centesimales, y podrás realizar conversiones entre estos sistemas de manera precisa.
- Aplicar las conversiones de ángulos: Serás capaz de convertir ángulos de un sistema de medida a otro (por ejemplo, de grados sexagesimales a radianes y viceversa) utilizando las fórmulas adecuadas.
- Utilizar ángulos en contextos prácticos: Podrás aplicar tus conocimientos sobre las medidas de ángulos en situaciones del mundo real, como en problemas de geometría, trigonometría y física.
- Interpretar y resolver problemas: Desarrollarás habilidades para interpretar y resolver problemas matemáticos y científicos que involucren el uso de diferentes medidas de ángulos, mejorando tu capacidad de pensamiento crítico y analítico.

CONTENIDO
Distribución de los ángulos notables en sexagesimales, radianes y centesimales.
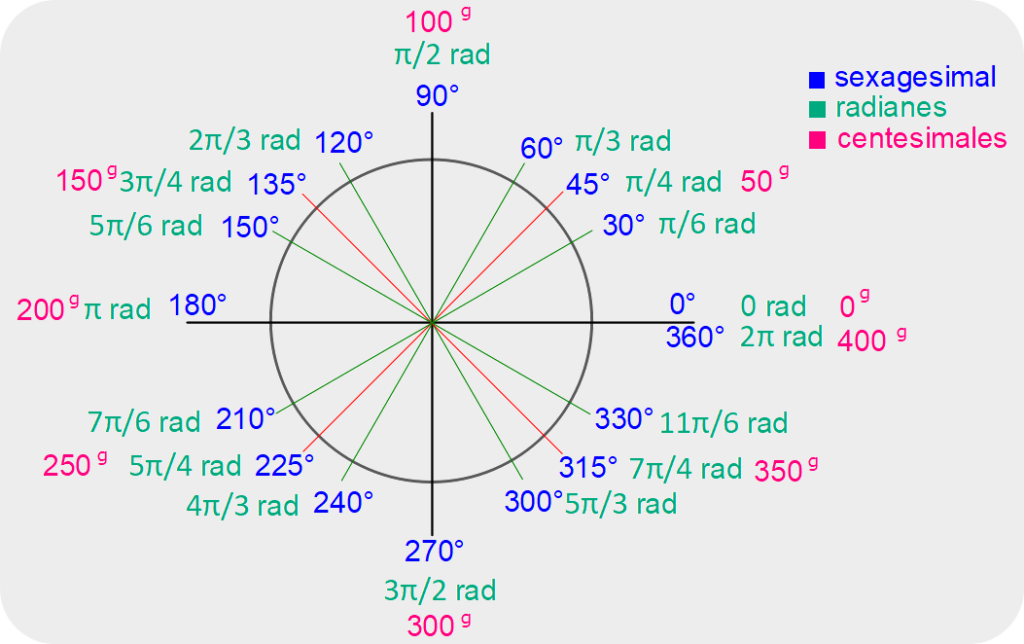
Ángulos sexagesimales
Es el sistema más común y se basa en dividir un círculo en 360 grados (°). Este método es utilizado en la mayoría de los contextos cotidianos y educativos.
El círculo está dividido en 360 partes iguales: 360°.
Cada cuadrante mide 90°, así que, si vamos completando los cuadrantes, comenzando por 0° avanzando de 90° en 90°, completamos el círculo: 0° (inicio), 90° (norte), 180° (oeste), 270° (sur), 360° (este – completa).
Si dividimos por la mitad a cada cuadrante, tendremos ángulos que avanzan de 45° en 45° que, comenzando por 0°, son: 0° (inicio), 45°, 90° (norte), 135°, 180° (oeste), 225°, 270° (sur), 315°, 360° (este – completa).
Si a cada cuadrante le dividimos en 3 partes iguales, obtenemos porciones de 30°. Comenzando por 0°, avanzando de 30° en 30°, completamos el círculo así: 0° (inicio), 30°, 60°, 90° (norte), 120°, 150°, 180° (oeste), 210°, 240°, 270° (sur), 300°, 330°, 360° (este – completa).
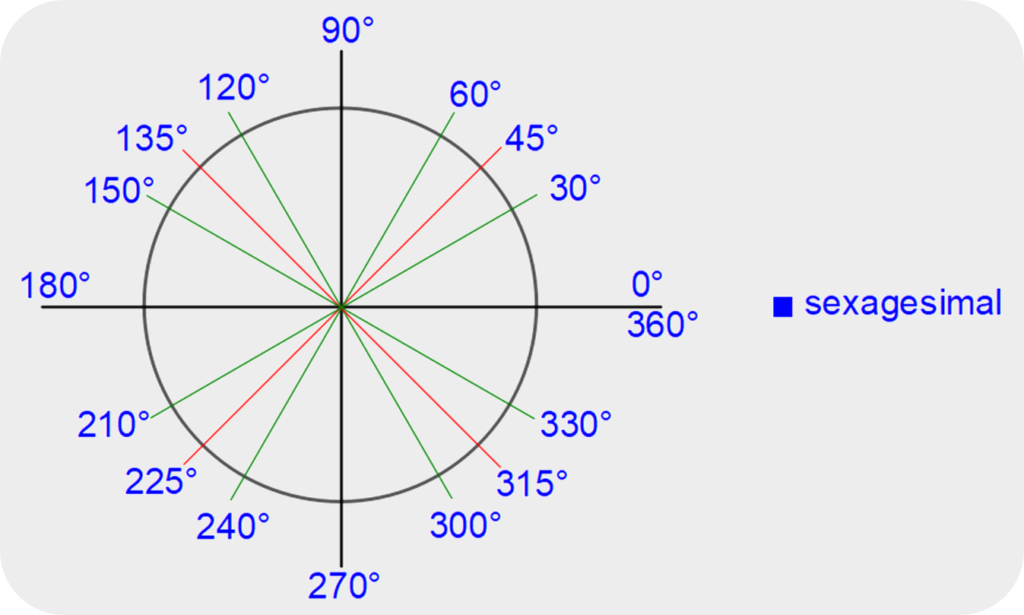
Radianes
Utilizados principalmente en matemáticas y física, los radianes son una unidad de medida basada en la longitud del arco de un círculo. Un radian equivale al ángulo subtendido por un arco cuya longitud es igual al radio del círculo.
El círculo está dividido en 2π partes iguales: 2π rad.
Cada cuadrante mide π/2 radianes (a los que simplemente llamaremos rad, o aún mejor, simplemente no ponemos la unidad). Si vamos completando los cuadrantes, comenzando por 0 rad, completamos el círculo: 0 rad (inicio), π/2 rad (norte), π (oeste), 3π/2 rad (sur), 2π rad (este – completa).
Si dividimos por la mitad a cada cuadrante, tendremos ángulos que avanzan de π/4 rad en π/4 rad que, comenzando por 0 rad, son: 0 rad (inicio), π/4 rad, π/2 rad (norte), 3π/4 rad, π (oeste), 5π/4 rad, 3π/2 rad (sur), 7π/4 rad, 2π rad (este – completa). Si a cada cuadrante le dividimos en 3 partes iguales, obtenemos porciones de π/6 rad. Comenzando por 0 rad, avanzando de π/6 rad en π/6 rad, completamos el círculo así: 0 rad (inicio), π/6 rad, π/3 rad, π/2 rad (norte), 2π/3 rad, 5π/6 rad, π (oeste), 7π/6 rad, 4π/3 rad, 3π/2 rad (sur), 5π/3 rad, 11π/6 rad, 2π rad (este – completa).
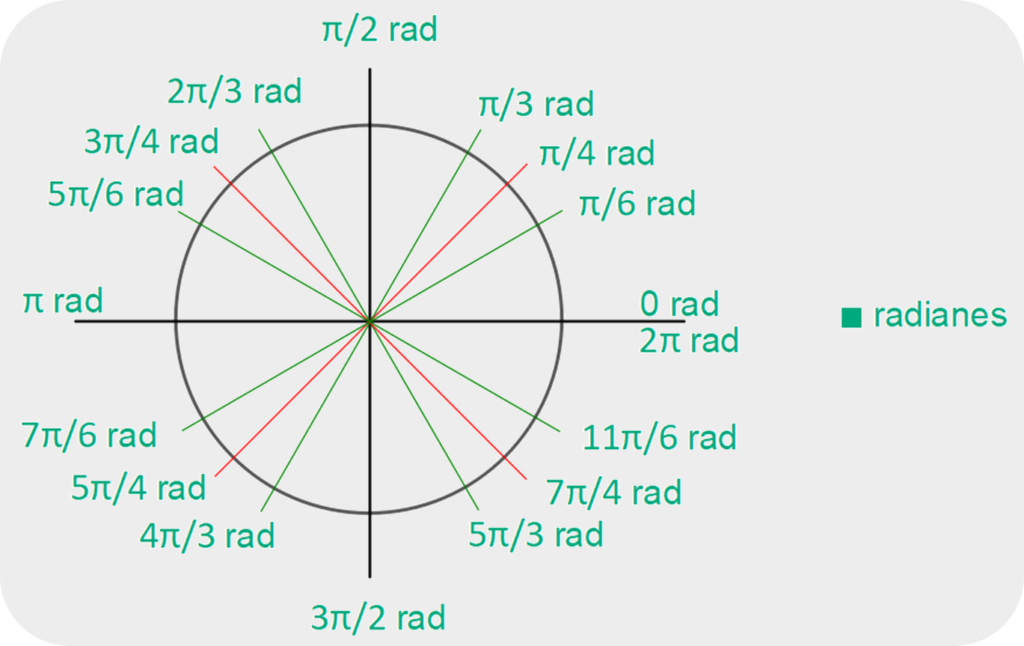
Ángulos centesimales
También conocidos como “grados centesimales” o “grados gon”, este sistema divide un círculo en 400 unidades, lo que facilita ciertos cálculos geométricos y de topografía.
El círculo está dividido en 400 partes iguales: 400g.
Cada cuadrante mide 100g, así que, si vamos completando los cuadrantes, comenzando por 0g avanzando de 100g en 100g, completamos el círculo: 0g (inicio), 100g (norte), 200g (oeste), 300g (sur), 400g (este – completa).
Si dividimos por la mitad a cada cuadrante, tendremos ángulos que avanzan de 50g en 50g que, comenzando por 0g, son: 0g (inicio), 100g (norte), 200g (oeste), 300g (sur), 400g (este – completa). Si a cada cuadrante le dividimos en 4 partes iguales, obtenemos porciones de 25g. Comenzando por 0g, avanzando de 25g en 25g, completamos el círculo así: 0g (inicio), 25 g, 50 g, 75 g, 100g (norte), 125 g, 150 g, 175 g, 200g (oeste), 225 g, 250 g, 275 g, 300g (sur), 325 g, 350 g, 375 g, 400g (este – completa).
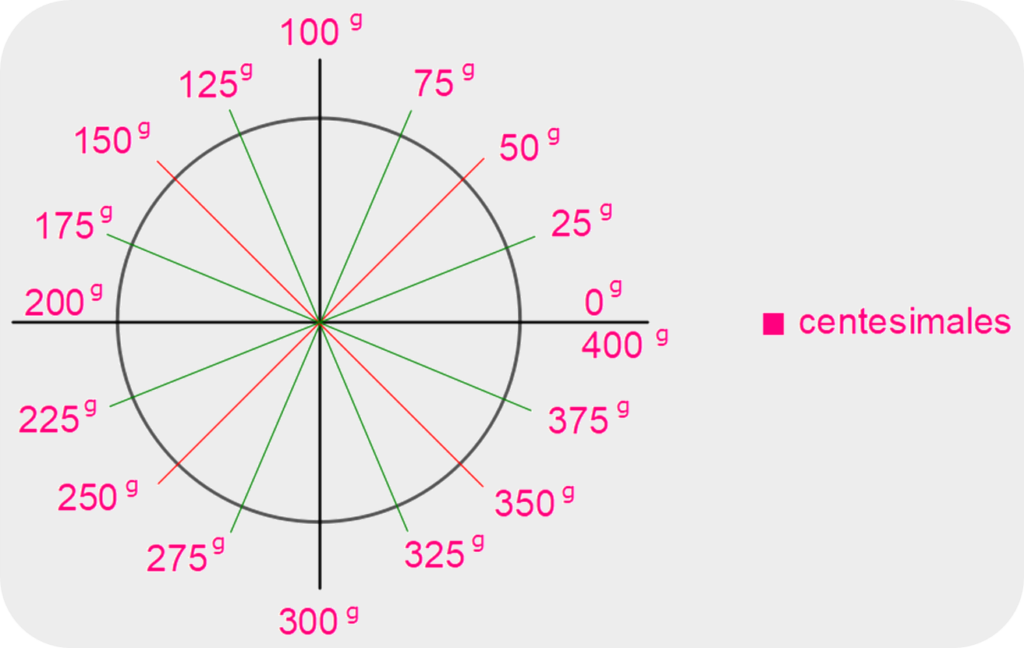
Conversiones de ángulos
Para poder convertir las unidades de un ángulo en otra equivalente, usaremos las siguientes equivalencias:
360° = 2π rad = 400g = 1 rev
Para realizar la conversión de una unidad a otra, realizaremos el siguiente mecanismo:
Colocamos la cantidad con su unidad, y al lado, abrimos una fracción. En esta fracción colocaremos las equivalencias, así: arriba (numerador) el valor de la equivalencia con la unidad a la que queremos llegar; y abajo (denominador) la equivalencia con la unidad del ejercicio original.
No te preocupes, te lo explico con los siguientes ejemplos:
Ejemplo 1:
Queremos convertir 248° en grados centesimales (g). Debido a que vamos a convertir de grados sexagesimales (°) a grados centesimales (g), usaremos las equivalencias que se encuentran resaltadas:
360° = 2π rad = 400g = 1 rev
Para convertir 248° en centesimales, escribimos 248°, y al lado colocamos la línea de fracción:
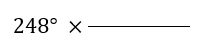
En el numerador ponemos la unidad a la que queremos llegar con su respectiva equivalencia, y en el denominador, la unidad igual a la del ejercicio plantado, con su respectiva equivalencia:
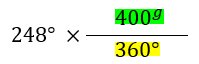
Operamos (multiplicamos los dos de arriba: 243×400, y dividimos para el de abajo: 360):

Entonces, 248° equivalen a 275.76g.
Las respuestas también pueden darse en decimales.
Ejercicios resueltos:
- Convertir 42° a radianes
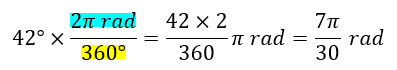
- Convertir a grados sexagesimales (°)
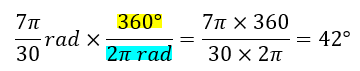
- Convertir 317° a grados centesimales (g)
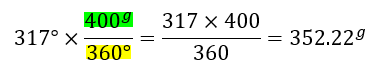
- Convertir 213g a grados sexagesimales (°)
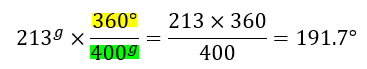
- Convertir a grados centesimales (g)
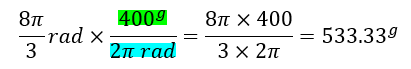
- Convertir 91g a radianes (rad)
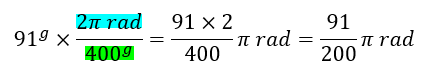
Ejercicios propuestos:

Aplicaciones

Ingeniería y Construcción: En la planificación y construcción de estructuras, los ingenieros usan frecuentemente ángulos en diferentes unidades. Por ejemplo, al diseñar una rampa o un puente, es posible que necesiten convertir entre grados sexagesimales (comúnmente usados en planos arquitectónicos) y radianes (usados en cálculos matemáticos y físicos).
Navegación y Geodesia: Los ángulos son fundamentales en la navegación marítima y aérea, así como en la cartografía. Los navegantes y topógrafos a menudo necesitan convertir entre grados sexagesimales (para coordenadas geográficas) y radianes (para cálculos de distancia y rumbo). Además, en la cartografía, los ángulos centesimales pueden ser usados para mayor precisión en ciertas situaciones.
Análisis de Señales y Sistemas de Control: En el campo de la ingeniería eléctrica y electrónica, las conversiones de ángulos son cruciales para el análisis de señales y en sistemas de control. Por ejemplo, al trabajar con ondas sinusoidales en el dominio del tiempo y la frecuencia, los ángulos se expresan frecuentemente en radianes. Sin embargo, para ciertas aplicaciones prácticas, como la calibración de equipos, puede ser necesario convertir estos valores a grados sexagesimales o centesimales.
