
¡Bienvenido al fascinante mundo de la trigonometría! ¿Te has preguntado alguna vez cómo los ingenieros calculan la altura de un edificio sin medirlo directamente? ¿O cómo los navegantes determinan su posición en el vasto océano con solo unas pocas estrellas? La respuesta está en las razones trigonométricas.
En esta lección, te sumergirás en la magia de los triángulos rectángulos y descubrirás cómo la trigonometría nos ayuda a resolver problemas del mundo real de manera sorprendentemente sencilla y precisa. Prepárate para desvelar los secretos de los ángulos y los lados de los triángulos, y a ver el mundo desde una nueva perspectiva matemática.
Learning Goals
- Comprender las razones trigonométricas: Aprenderás a definir las razones trigonométricas básicas (seno, coseno y tangente) y entenderás su relación con los ángulos y lados de un triángulo rectángulo.
- Calcular razones trigonométricas: Serás capaz de calcular el seno, coseno y tangente de ángulos agudos en triángulos rectángulos usando longitudes de los lados.
- Aplicar razones trigonométricas: Aprenderás a utilizar las razones trigonométricas para resolver problemas prácticos, como encontrar alturas y distancias sin medirlas directamente.
- Identificar y utilizar razones trigonométricas inversas: Serás capaz de utilizar las funciones trigonométricas inversas (arcseno, arccoseno, arctangente) para encontrar ángulos cuando conoces las longitudes de los lados.
- Visualizar y representar triángulos rectángulos: Podrás dibujar y etiquetar triángulos rectángulos correctamente, representando las razones trigonométricas de manera clara y precisa.
CONTENIDO
Importancia
Las razones trigonométricas son herramientas esenciales en muchos campos, desde la ingeniería y la arquitectura hasta la navegación y la astronomía. Nos permiten calcular distancias, alturas y ángulos de manera precisa y eficiente, sin necesidad de mediciones directas. Además, el estudio de la trigonometría desarrolla tus habilidades de pensamiento lógico y resolución de problemas, competencias valiosas en cualquier área del conocimiento. Al dominar estas razones, no solo mejorarás tu comprensión de la geometría, sino que también abrirás las puertas a un mundo de aplicaciones prácticas y avanzadas en matemáticas y ciencias.
Las razones trigonométricas
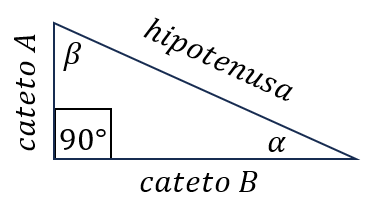
Un triángulo rectángulo está compuesto por 3 lados y 3 ángulos. Los 3 lados corresponden a 2 lados menores llamados catetos (que forman el ángulo de 90°) y la hipotenusa, que une a los catetos. La hipotenusa es el lado más grande, y que cada uno de los dos catetos.
En cuanto a los 3 ángulos, uno de ellos, opuesto a la hipotenusa, es de 90°, al que se suele representar con un cuadrado pequeño.
Las razones trigonométricas dependen del ángulo que se esté analizando.
Es un error definir uno de los catetos como opuesto y el otro como adyacente de forma fija. Generalmente, cuando se pregunta a los estudiantes cuál es el cateto opuesto y cuál es el adyacente, inmediatamente responden que el opuesto es el cateto vertical, y el adyacente es el horizontal. Sin embargo, esto no es así, pues el “cateto opuesto” y el “cateto adyacente” toman su nombre según el ángulo al que se esté haciendo referencia.
Cateto opuesto: es uno de los lados menores del triángulo que está al frente del ángulo que se está analizando. Es decir, es el lado que no toca para nada al ángulo que se está analizando. Por ejemplo, para el triángulo a continuación, si estamos analizando el ángulo al que le hemos puesto , el cateto opuesto es el cateto A, puesto que están al frente uno del otro. Por otro lado, si el ángulo que estamos analizando fuera el ángulo al que hemos llamado , el cateto opuesto a este sería el cateto B, puesto que están frente a frente.
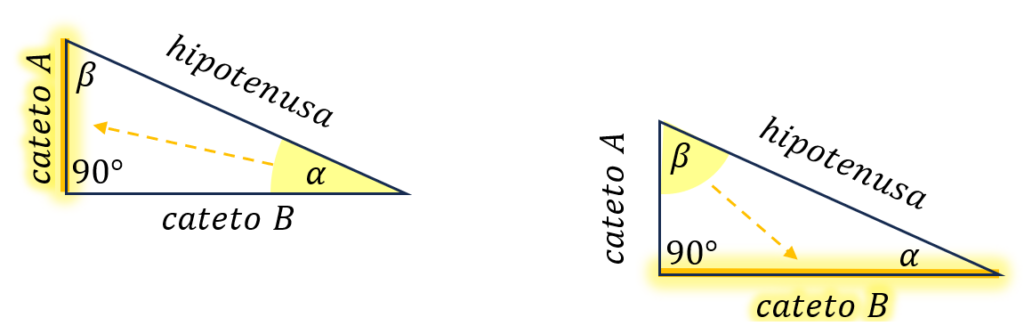
Cateto adyacente: es uno de los lados menores del triángulo que está al lado del ángulo que se está analizando (la hipotenusa no cuenta como cateto). Es decir, es el lado (cateto) que sí toca al ángulo que se está analizando. Por ejemplo, para el triángulo a continuación, si estamos analizando el ángulo al que le hemos puesto , el cateto adyacente es el cateto B, puesto que se están “tocando”. Por otro lado, si el ángulo que estamos analizando fuera el ángulo al que hemos llamado , el cateto adyacente a este sería el cateto A, puesto que se están “tocando”.
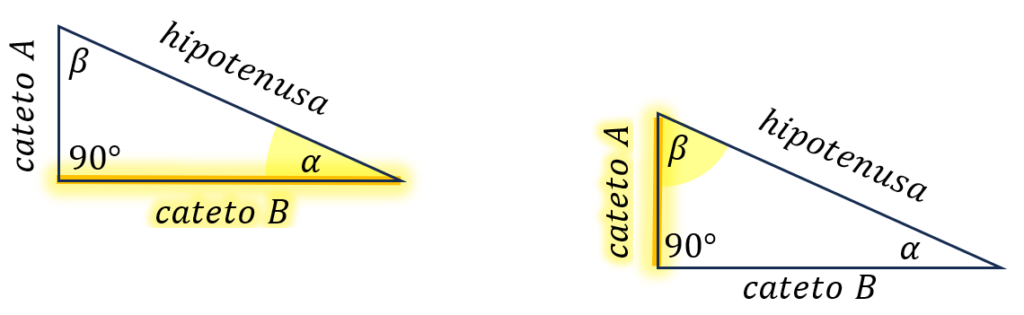
Razones trigonométricas

Ejemplos:
Ejemplo 1:
Halla las razones trigonométricas para cada ángulo del siguiente triángulo:
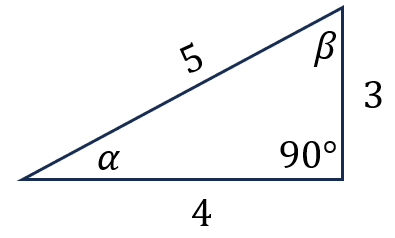
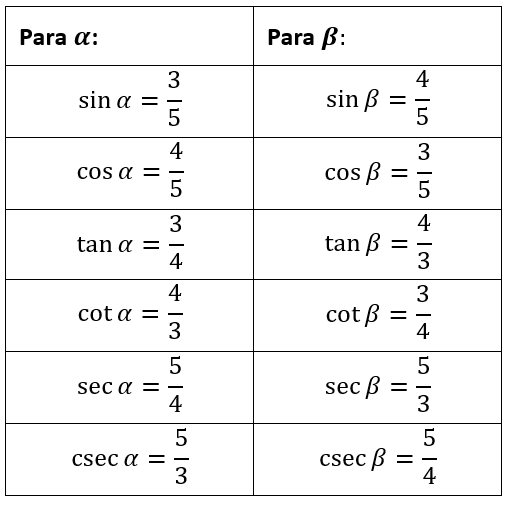
Ejemplo 2:
Halla las razones trigonométricas para cada ángulo del siguiente triángulo:
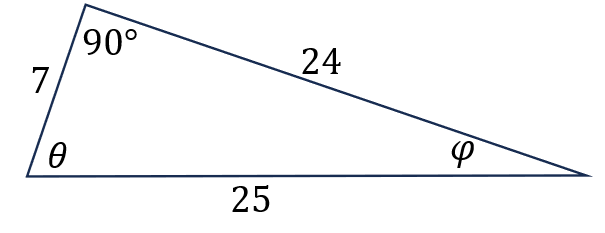
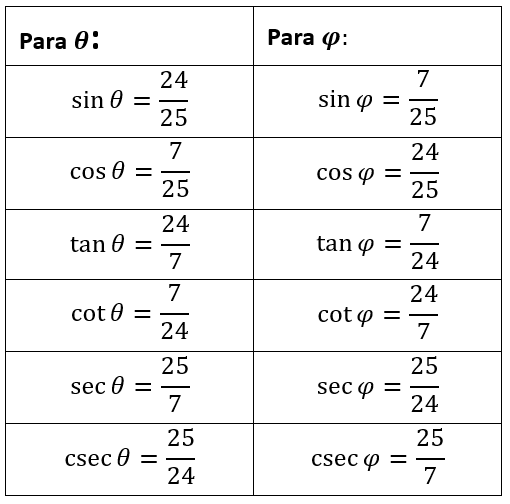
Ejercicios propuestos:
Ejercicio propuesto 1:
Halla las razones trigonométricas para cada ángulo del siguiente triángulo:
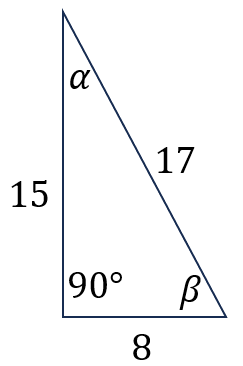
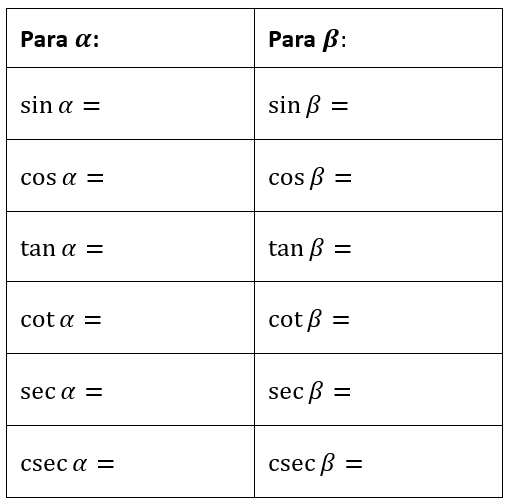
Ejercicio propuesto 2:
Halla las razones trigonométricas para cada ángulo del siguiente triángulo:
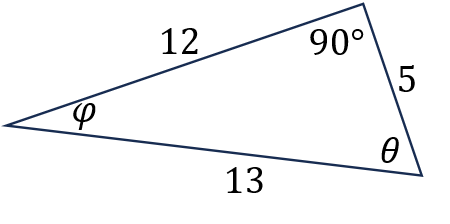

Aplicaciones

Navegación y Cartografía 🧭
- Descripción: Los marineros y pilotos utilizan la trigonometría para calcular distancias y determinar su posición exacta en el mapa mediante la triangulación. Las razones trigonométricas, como el seno, el coseno y la tangente, son fundamentales para estos cálculos.
- Ejemplo: Determinar la distancia entre dos puntos en el mar conociendo un ángulo y una distancia inicial.
Ingeniería y Construcción 🏗️
- Descripción: Los ingenieros y arquitectos emplean la trigonometría para diseñar y construir edificios, puentes y carreteras. Ayuda a calcular alturas, longitudes y ángulos precisos necesarios para la estabilidad y funcionalidad de las estructuras.
- Ejemplo: Calcular la altura de un edificio utilizando la sombra proyectada y el ángulo de elevación del sol.
Astronomía 🌌
- Descripción: Los astrónomos usan la trigonometría para medir la distancia entre estrellas y planetas, y para determinar la magnitud de los cuerpos celestes. Esto es posible gracias a técnicas como la paralaje y la ley de los senos.
- Ejemplo: Calcular la distancia de la Tierra a una estrella cercana usando el ángulo de observación desde dos puntos diferentes en la órbita terrestre.
