
Las medidas de dispersión nos ayudan a entender cómo se distribuyen los datos alrededor de una medida de tendencia central, como la media. Nos indican qué tan dispersos o concentrados están los datos.
Las medidas más comunes de dispersión son el rango, la varianza y la desviación estándar. A continuación, veremos cómo calcular cada una de estas medidas y su importancia con ejemplos prácticos.
Learning Goals
- Comprender el concepto de dispersión: Serás capaz de explicar qué significa la dispersión en un conjunto de datos y por qué es importante para entender la variabilidad de los datos.
- Calcular el rango: Aprenderás a calcular el rango de un conjunto de datos no agrupados y entenderás cómo esta medida muestra la diferencia entre el valor máximo y el valor mínimo.
- Determinar la varianza: Serás capaz de calcular la varianza de un conjunto de datos no agrupados y comprenderás cómo esta medida refleja la dispersión de los datos respecto a la media.
- Calcular la desviación estándar: Aprenderás a calcular la desviación estándar de un conjunto de datos no agrupados y entenderás cómo esta medida proporciona una visión de la dispersión en las mismas unidades que los datos originales.
- Aplicar medidas de dispersión: Podrás utilizar las medidas de rango, varianza y desviación estándar para analizar y comparar la variabilidad de diferentes conjuntos de datos en diversas situaciones prácticas.
CONTENIDO
Rango
El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Es la medida más simple de dispersión.
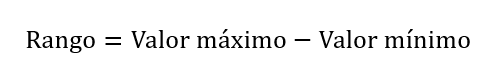
Ejemplo:
Supongamos que tenemos las siguientes edades de un grupo de estudiantes: 12, 14, 15, 13, 12.
- Valor máximo: 15
- Valor mínimo: 12
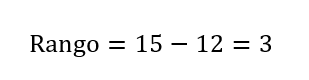
Varianza s2
La varianza mide la dispersión de los datos respecto a la media. Es el promedio de las diferencias al cuadrado entre cada valor y la media.
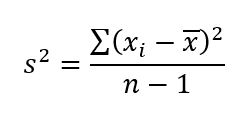
Donde xi es cada valor, es x con a ceja encima es la media, y n es el número de datos.
Ejemplo:
Para las edades 12, 14, 15, 13, 12, calculamos primero la media:
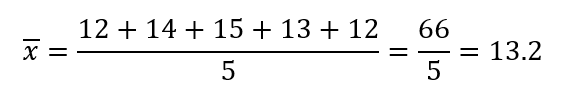
Luego, calculamos la varianza:
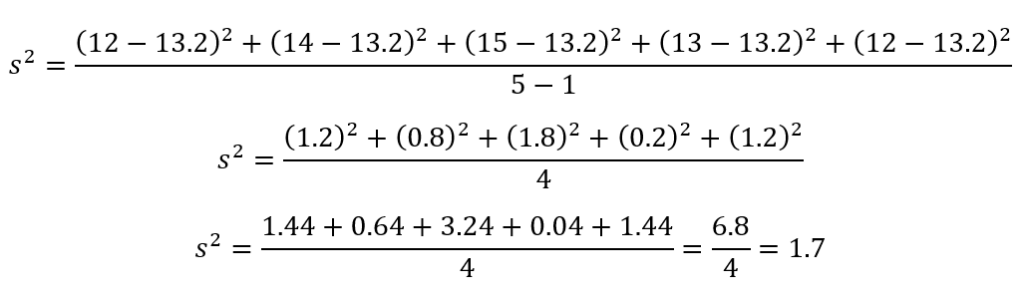
Desviación estándar o típica s
La desviación estándar es la raíz cuadrada de la varianza. Nos indica qué tan dispersos están los datos respecto a la media en las mismas unidades que los datos originales.
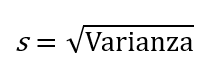
Ejemplo:
Utilizando la varianza calculada anteriormente:
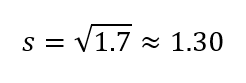
Ejemplo completo:
Consideremos el siguiente conjunto de datos de las notas de un examen de matemáticas: 7, 8, 7, 6, 9, 10, 6, 8, 7.
Rango:
- Valor máximo: 10
- Valor mínimo: 6
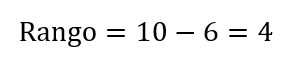
Varianza:
Calculamos primero la media:
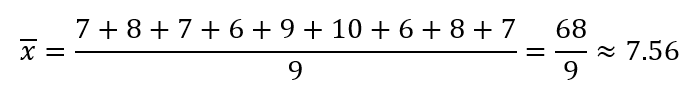
Luego, calculamos la varianza:
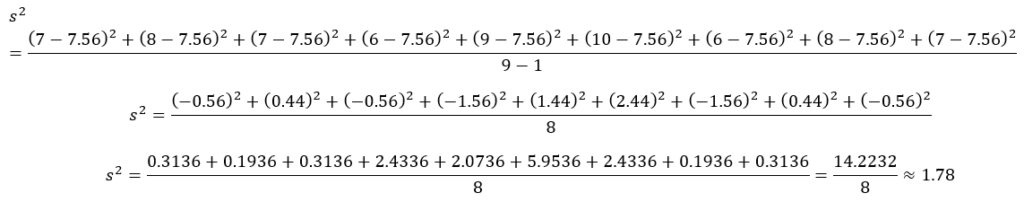
- Desviación Estándar:
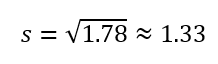
Aplicaciones

- Control de Calidad en la Industria:
- La desviación estándar se utiliza para medir la variabilidad en la producción de bienes. Por ejemplo, en una fábrica de botellas, una baja desviación estándar en el tamaño o peso asegura que los productos cumplen con los estándares y reduce los desperdicios.
- Análisis de Riesgo en Finanzas:
- Las medidas de dispersión como la varianza y la desviación estándar ayudan a evaluar el riesgo de inversiones. Una alta desviación estándar en los retornos de una acción indica mayor volatilidad, lo que puede implicar un mayor riesgo para los inversores.
- Evaluación del Rendimiento Académico:
- En el ámbito educativo, las medidas de dispersión ayudan a entender la uniformidad del desempeño de los estudiantes en una prueba. Una baja desviación estándar sugiere que los puntajes están cerca de la media, mientras que una alta indica una amplia variedad en el rendimiento.
Estas medidas son esenciales para comprender la variabilidad en datos y tomar decisiones fundamentadas.
