¿Alguna vez te has preguntado cómo los superhéroes obtienen sus poderes increíbles? Bueno, en el mundo de las matemáticas, las potencias son como los superpoderes de los números. Imagínate poder multiplicar un número por sí mismo varias veces con solo un par de trazos del lápiz. En esta lección, vamos a explorar las potencias y sus propiedades, y descubrir cómo podemos usar estos “superpoderes” para hacer cálculos de manera más rápida y eficiente. ¡Prepárate para convertirte en un verdadero héroe de las matemáticas! 🚀✨

Learning Goals
- Entender qué es la potenciación: Los estudiantes comprenderán los conceptos de base y exponente, así como la notación y el significado de una potencia.
- Conocer las propiedades de las potencias: Se explicarán las propiedades fundamentales de las potencias, como el producto y la potencia de una potencia, facilitando su comprensión.
- Practicar con ejercicios: Los estudiantes resolverán ejercicios simples que les permitirán aplicar las propiedades de las potencias y simplificar expresiones de manera efectiva.
- Resolver problemas: Los alumnos aplicarán sus conocimientos en la resolución de problemas matemáticos, desarrollando habilidades críticas y analíticas.
CONTENIDO
¿Qué es la potenciación?
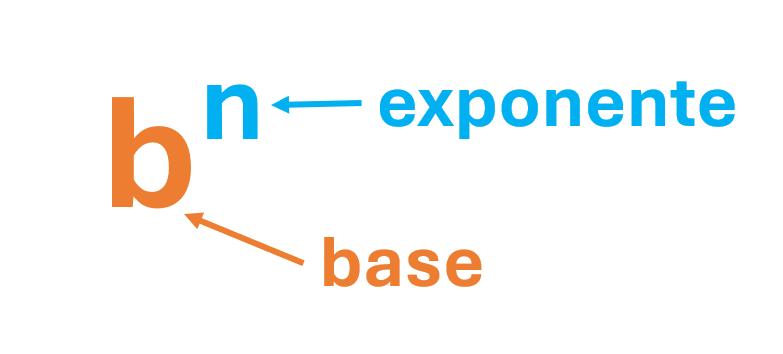
La potenciación es una operación matemática que nos permite multiplicar un número por sí mismo varias veces. En una potencia, el número que se multiplica se llama base, y el número de veces que se multiplica se llama exponente.
Al resultado de esta operación se le llama potencia.
Ejemplos:




Propiedades de la potenciación
Las propiedades de la potenciación se usan en doble vía; es decir, que puedes aplicarlas tanto al derecho como al revés.
Conceptos elementales
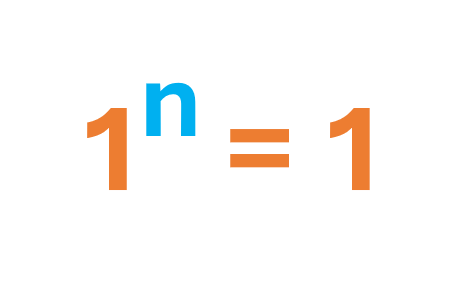
Base 1, elevada a cualquier exponente, es igual a 1.
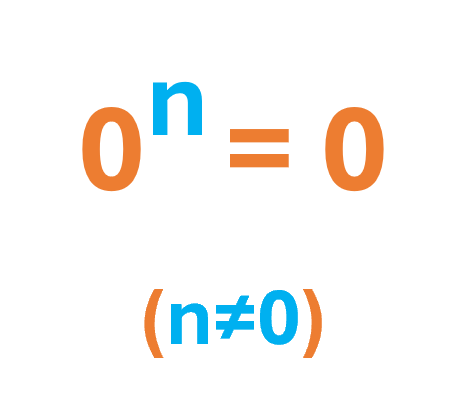
Base 0, elevada a cualquier exponente (excepto el 0 mismo), es igual a 0.
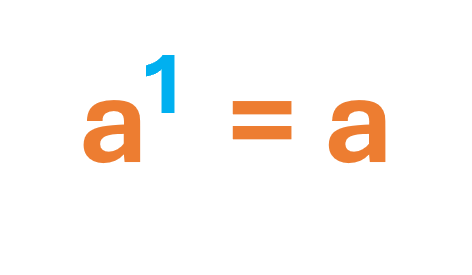
Cualquier valor de base elevada al exponente 1, es igual a la misma base a.
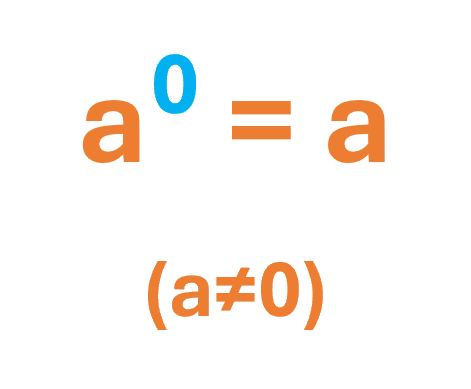
Cualquier valor base (excepto 0), elevada al exponente 0, es igual a 1.
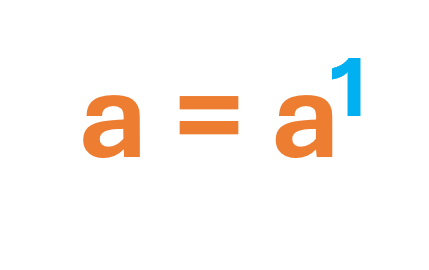
Toda expresión, por defecto, tiene exponente 1.
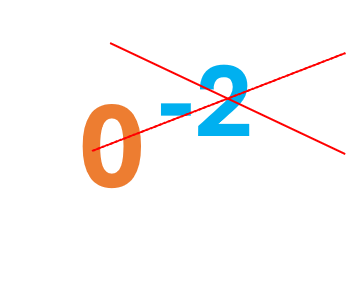
Base 0 no puede estar elevado a un número negativo.
1. Producto de potencias de igual base
Cuando dos o más bases iguales se multiplican entre sí, se conserva la base y se suman sus exponentes.
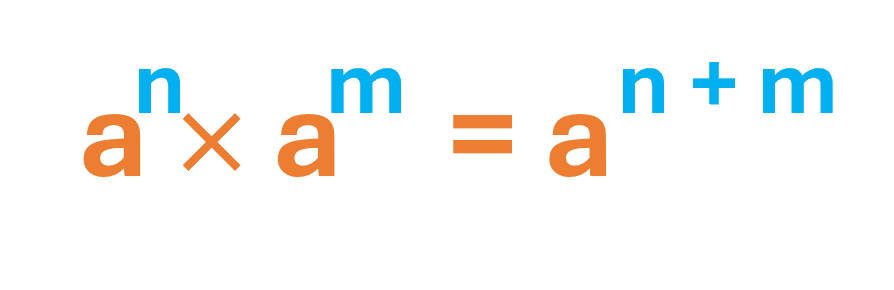
Ejemplos:
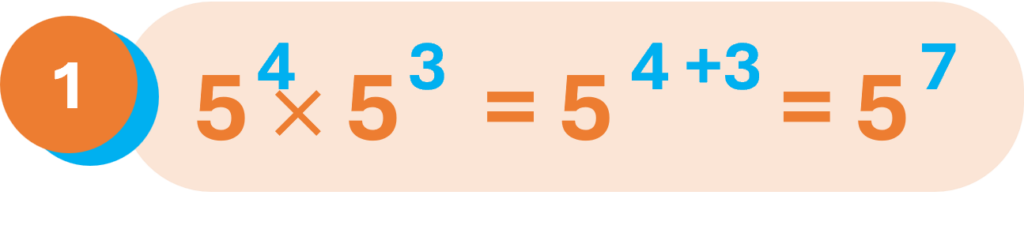
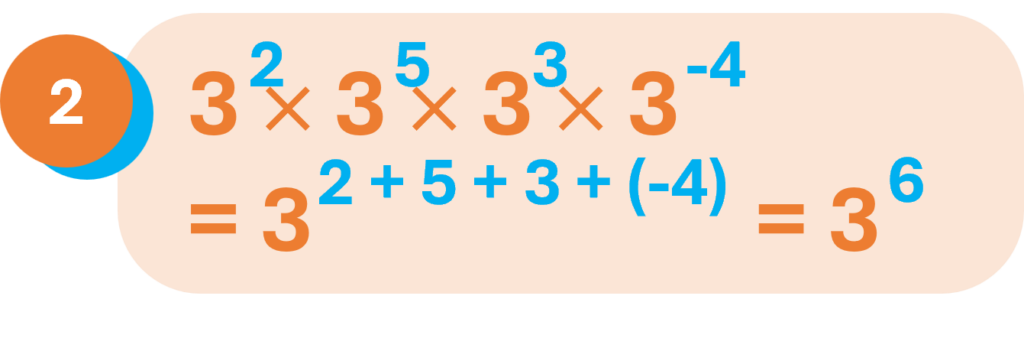
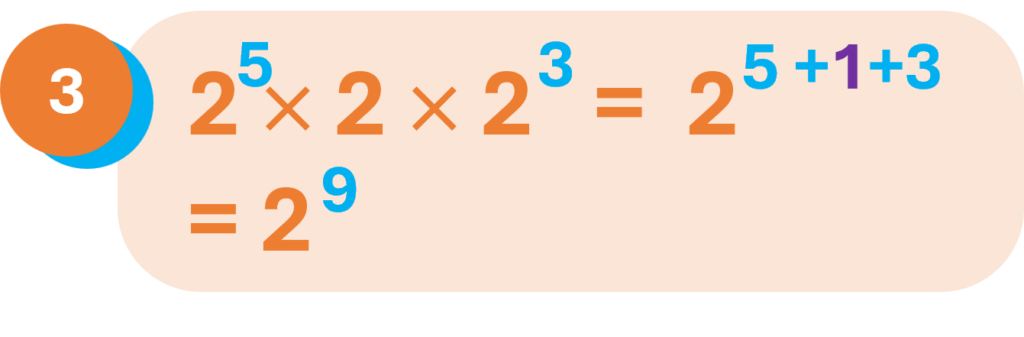
Nota que, en el ejemplo 3, la base 2 del medio tiene exponente 1, que normalmente no se lo escribe, pero se sabe que está allí (revisa la sección “Conceptos elementales” que está más arriba).
2. Cociente de potencias de igual base
Cuando dos o más bases iguales se dividen entre sí, se conserva la base y se restan sus exponentes (exponente del numerador menos exponente del denominador).
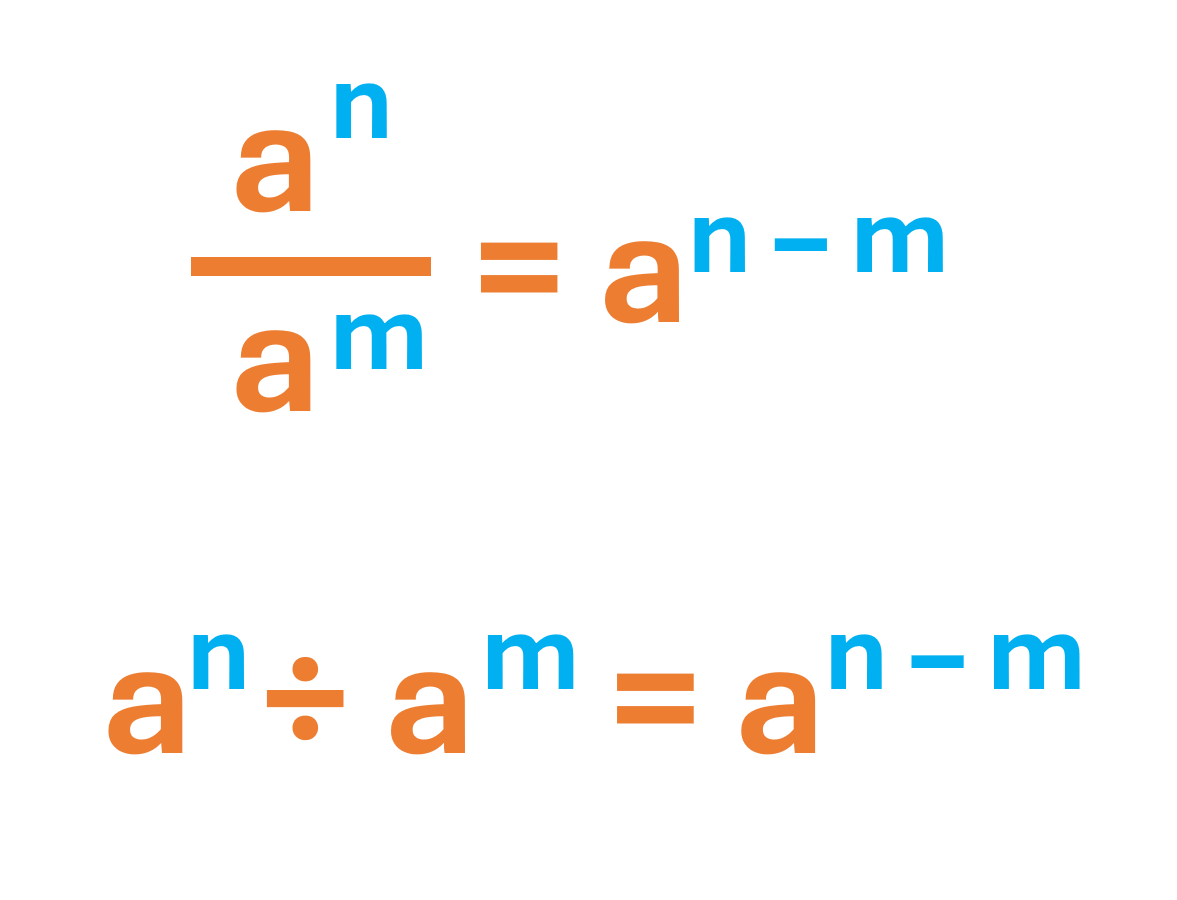
Ejemplos:
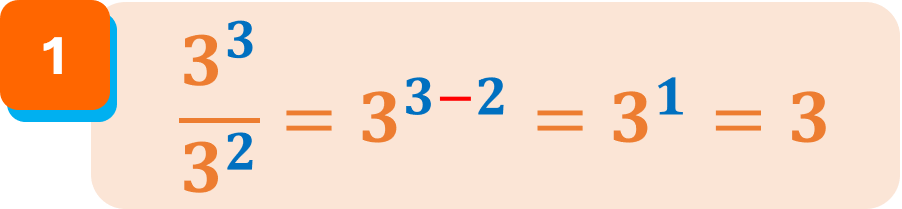
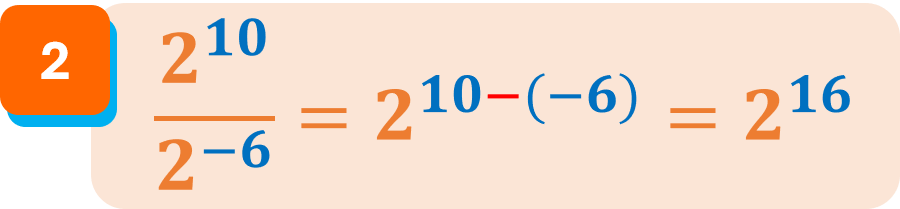
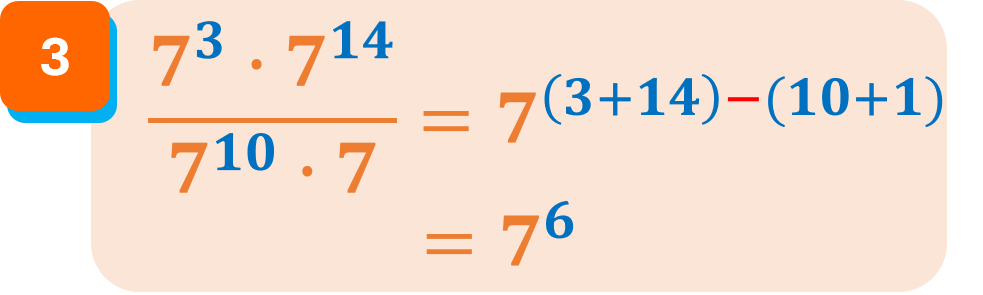

3. Potencia de un producto
Cuando dos o más bases que multiplican entre sí, están elevadas a una potencia, esta se reparte para cada una de forma distributiva.
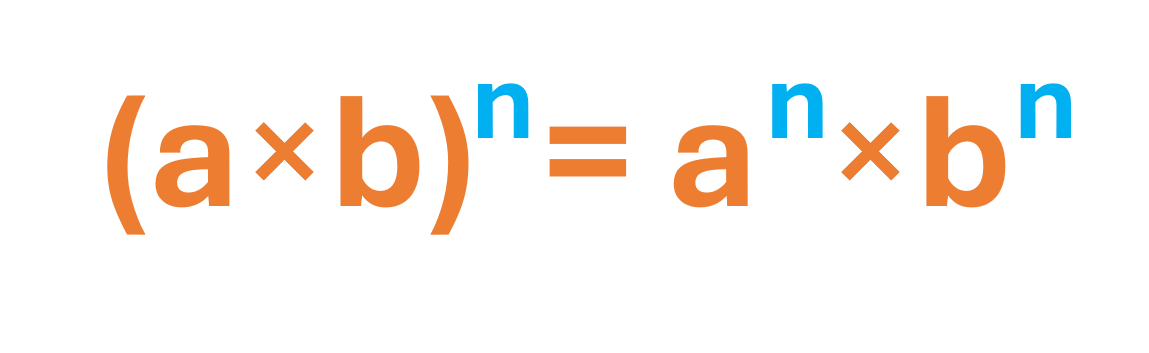
Ejemplos:
4. Potencia de un cociente
Cuando dos o más bases iguales se multiplican entre sí, se conserva la base y se suman sus exponentes.
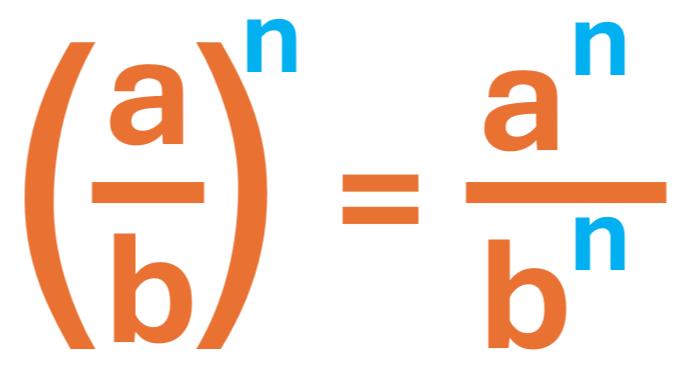
Ejemplos:
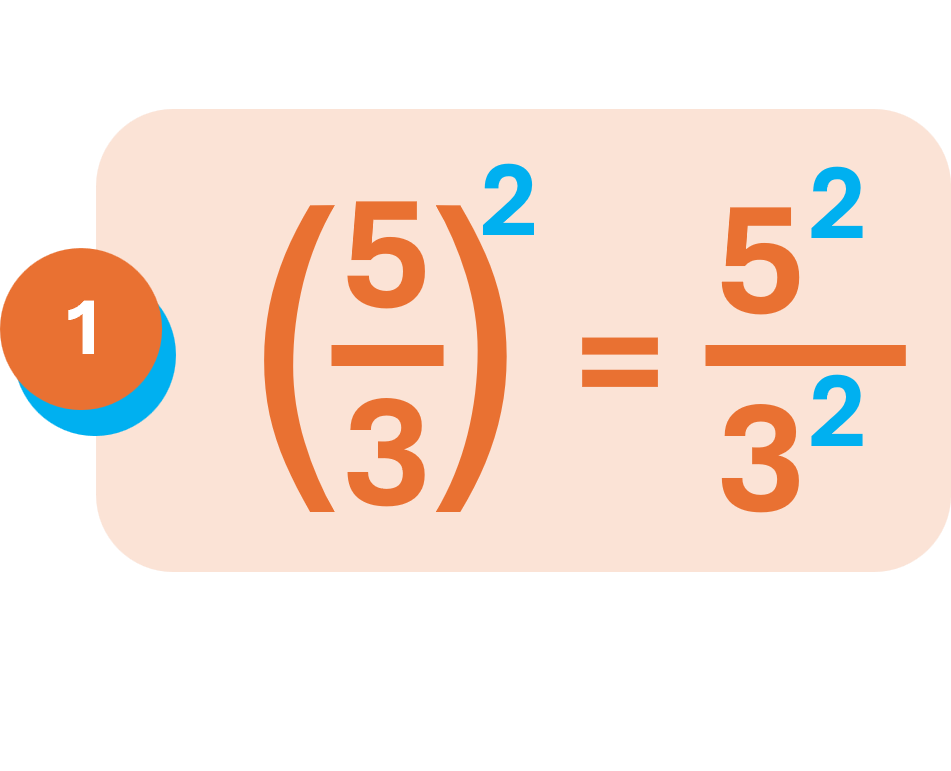
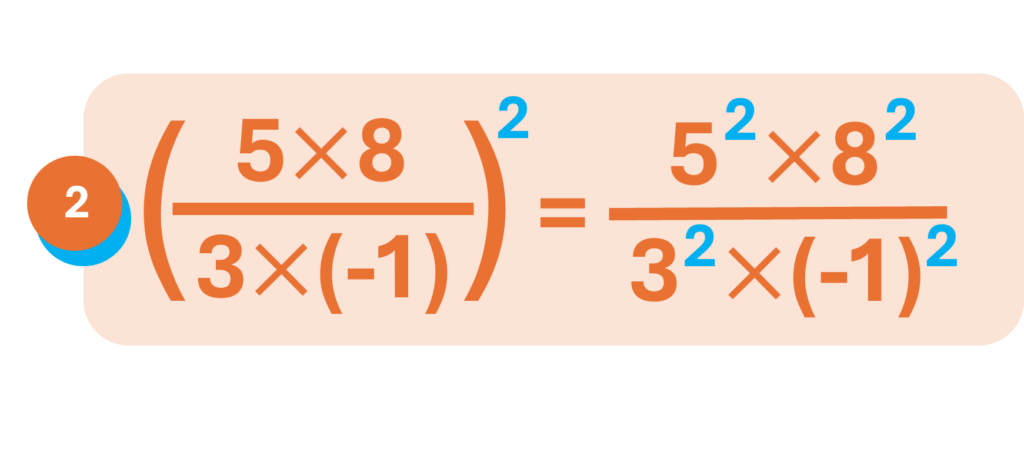
6. Potencia de potencia
Cuando dos o más bases iguales se multiplican entre sí, se conserva la base y se suman sus exponentes.
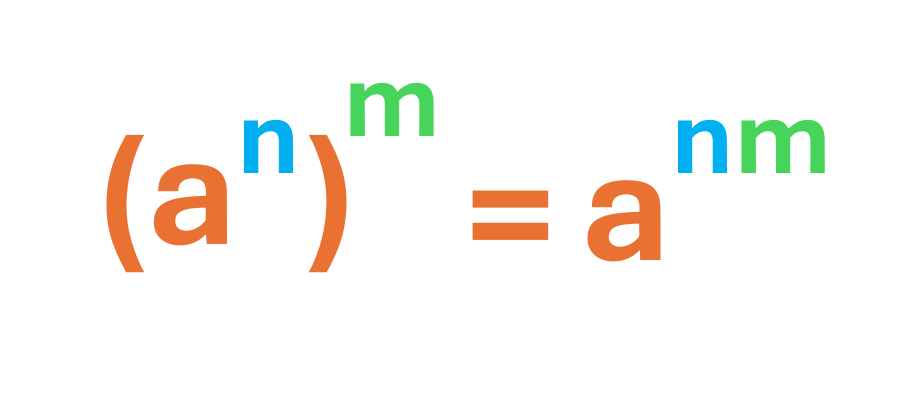
Ejemplos:
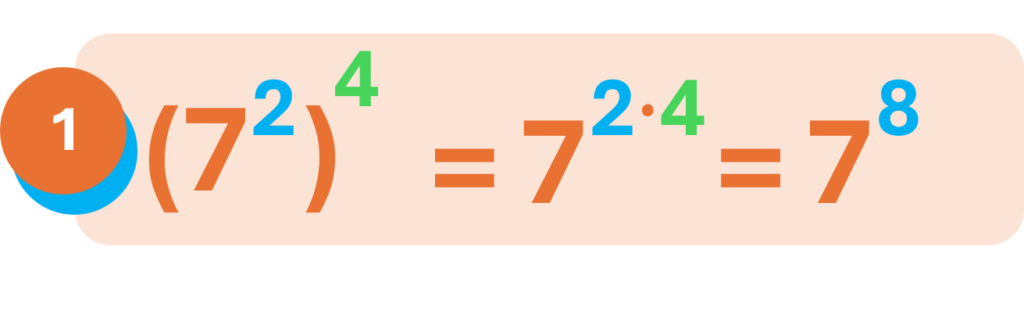
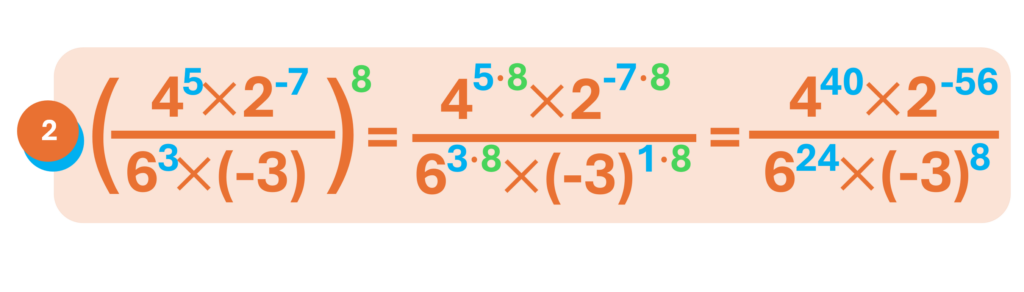
Aplicaciones prácticas
1. Crecimiento de la población de bacterias
Imagina que tienes una bacteria en un laboratorio, y cada hora esta se divide en dos bacterias. Después de 1 hora tienes 2 bacterias, después de 2 horas tienes 4 bacterias, y así sucesivamente. El número total de bacterias después de “5” horas se calcula como 25=32 bacterias. Es una forma de entender cómo la potenciación describe crecimientos rápidos, como el de algunos microorganismos.
2. Expansión de redes sociales
Imagina que compartes una publicación interesante en redes sociales. Si cada persona que ve tu publicación la comparte con otras 3 personas, y esas 3 la comparten con otras 3, el alcance crece exponencialmente para cada nuevo grupo de personas según 3n. Así es como los contenidos virales se esparcen rápidamente.

3. Pirámide de energía (análisis inverso)
En este análisis inverso, los consumidores terciarios, como jaguares, requieren (101 = 10) unidades de energía. Los secundarios, como serpientes, necesitan (102 = 100) unidades, alimentándose de recursos del nivel anterior. Los primarios, como conejos, consumen (103 = 1,000) unidades al alimentarse de plantas. Finalmente, los productores, como las plantas, generan (104 = 10,000) unidades mediante fotosíntesis, que sostienen el ecosistema.

