
Imagina que estás subiendo una colina en bicicleta. La inclinación del terreno determina lo difícil que será tu ascenso. De la misma manera, la pendiente de una recta en matemáticas nos dice cuán empinada es esa “colina” en un gráfico. La pendiente es una herramienta clave para entender cómo cambian las cosas a medida que nos movemos a lo largo de una línea, ya sea el crecimiento de una población, el costo de un producto, o la velocidad de un automóvil. En esta lección, descubrirás cómo calcular y aplicar la pendiente de una recta en diferentes contextos del mundo real.
Learning Goals
- Definir qué es la pendiente de una recta y cómo se calcula.
- Comprender la relación entre la pendiente y la inclinación de una recta.
- Aplicar el concepto de pendiente a problemas y situaciones del mundo real.
- Desarrollar habilidades para interpretar gráficas de rectas y utilizar la pendiente en análisis matemático.
- Analizar cómo la pendiente afecta las decisiones y resultados en diferentes campos.
CONTENIDO
Signo de la pendiente y su representación
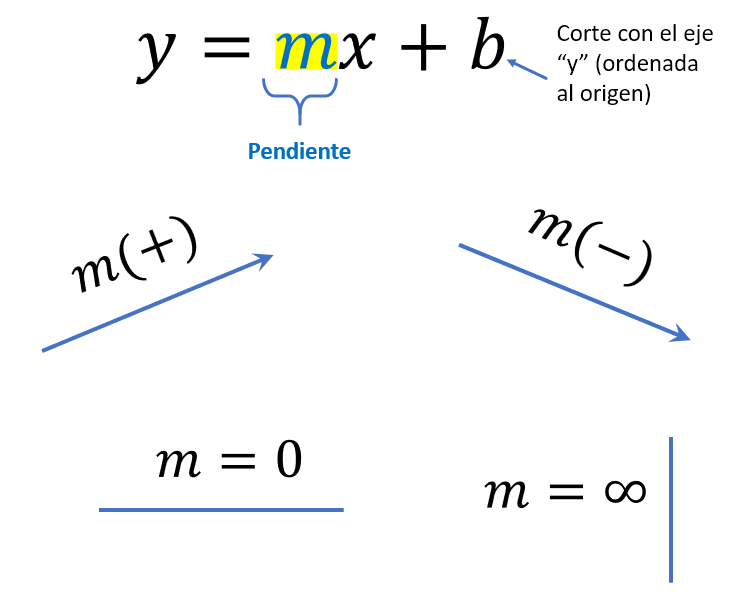
Cómo se obtiene la pendiente
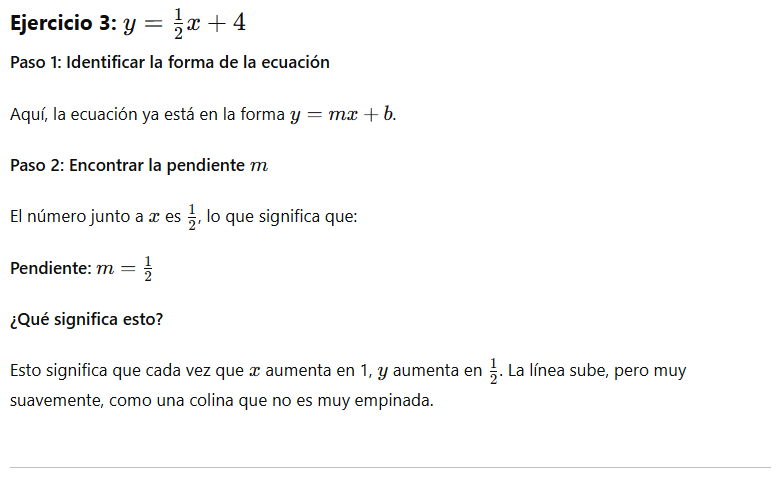
Identificándola en la ecuación explícita





Dados dos puntos





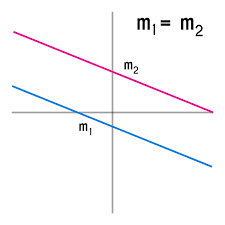
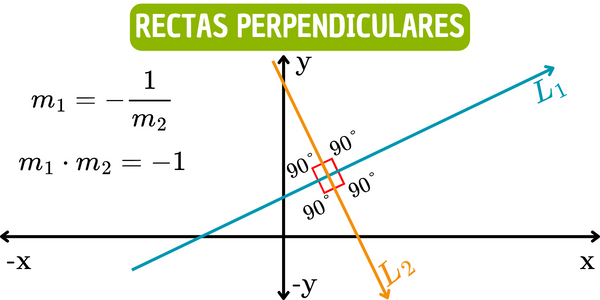
Perpendicularidad y paralelismo
Relación de pendientes en rectas paralelas
Relación de pendientes en rectas perpendiculares
Rectas secantes
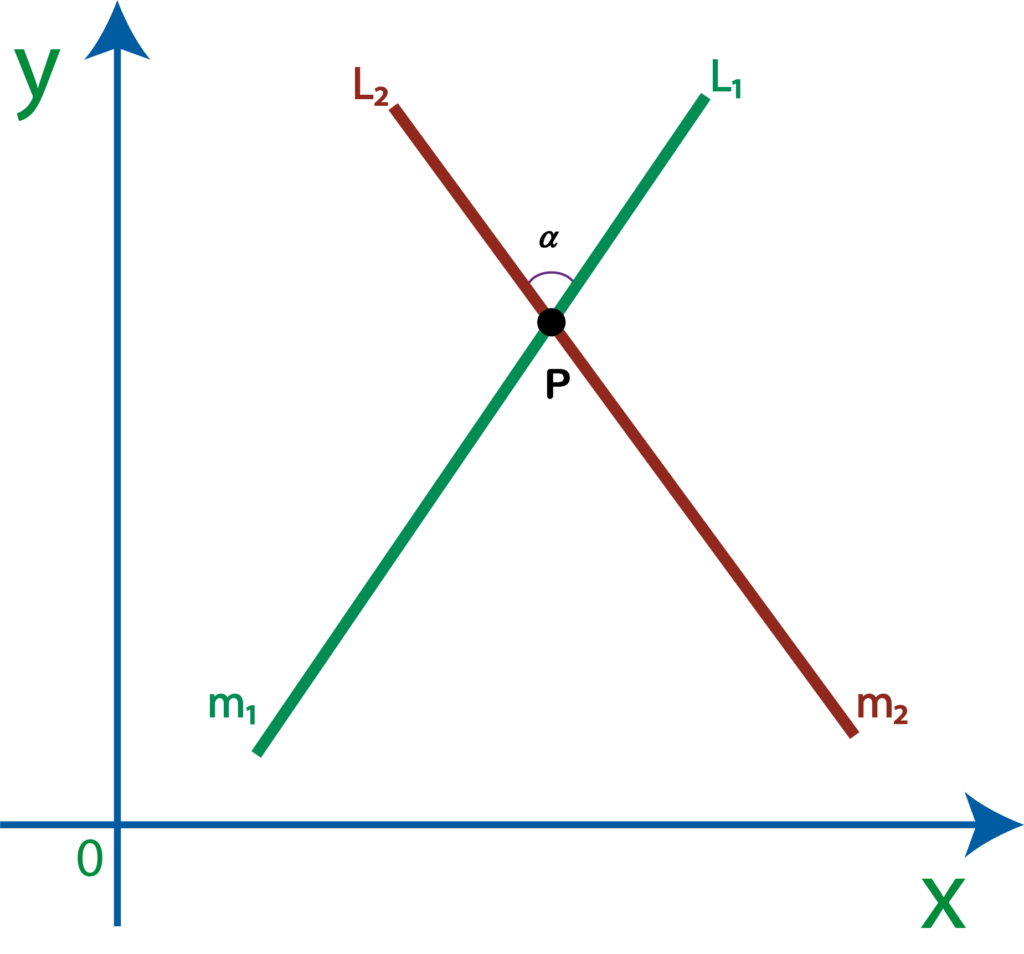
Identificando el tipo de rectas por la relación de sus pendientes
Aplicaciones

- Ingeniería Civil: La pendiente es crucial para diseñar carreteras y rampas, asegurando que sean seguras y accesibles para vehículos y peatones.
- Economía: Los economistas utilizan la pendiente para analizar la relación entre oferta y demanda en el mercado, prediciendo cómo los precios cambiarán.
- Deportes: En atletismo, la pendiente de una pista de carreras puede afectar el rendimiento de los corredores, especialmente en eventos de campo traviesa.
- Arquitectura: Los arquitectos calculan la pendiente al diseñar techos inclinados, para garantizar que el agua de lluvia se drene correctamente.
- Ciencia de Datos: En modelos de regresión lineal, la pendiente representa la relación entre variables, permitiendo predicciones y análisis de tendencias.
actividades
- Carrera de Pendientes: Los estudiantes competirán para resolver problemas de pendiente, subiendo en una “escalera” cada vez que calculen correctamente la pendiente de una recta dada.
- Desafío de Construcción: Utilizando bloques o gráficos interactivos, los estudiantes deberán construir rampas con pendientes específicas para alcanzar objetivos predeterminados.
- Juego de Oferta y Demanda: Simula un mercado donde los estudiantes deben ajustar la pendiente de la curva de oferta y demanda para maximizar beneficios o minimizar pérdidas.
- Escape Room Matemático: Diseña un escape room donde los estudiantes deben calcular pendientes para “escalar” diferentes niveles y avanzar en el juego.
- Competencia de Proyectos: Los estudiantes trabajarán en equipos para diseñar un proyecto (como una rampa o un techo) utilizando el concepto de pendiente. Los equipos presentarán sus proyectos y se otorgarán puntos por precisión y creatividad.
recursos adicionales
- Khan Academy: Introduction to Slope
- Desmos: Slope Calculator
- [YouTube: Understanding Slope](https://www.youtube.com/watch?v=Ba
Conclusiones
Este contenido te guiará a través del aprendizaje de la pendiente de una recta de manera clara y accesible, ayudándote a dominar un concepto fundamental en matemáticas y en la vida cotidiana. ¡Prepárate para ver el mundo desde una nueva perspectiva matemática!
