Método de reducción

---

Imagina que estás organizando una fiesta y necesitas decidir cómo distribuir a tus invitados en las mesas. Cada mesa tiene un número limitado de sillas y quieres que todos tengan un lugar. Aquí es donde entra en juego el método de Reducción para sistemas de ecuaciones lineales.

Este método es como ser un detective matemático. Tienes varias pistas (las ecuaciones) y tu misión es descubrir cómo distribuir a los invitados (las soluciones). Usamos pasos lógicos para simplificar el sistema y encontrar las soluciones de manera ordenada. ¡Prepárate para convertirte en un estratega matemático! 🚀

¿Listo para empezar?

Learning Goals

1. Simplificar las ecuaciones para que sean más fáciles de resolver.
2. Eliminar variables de manera ordenada.
3. Encontrar soluciones precisas para cada variable.
4. Verificar que las soluciones sean correctas.
5. Aplicar el método a problemas prácticos.

---

CONTENIDO

Reglas

Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.

Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.

Para el Método de Reducción, procederemos así:

1. Multiplicar para igualar coeficientes. Ajusta una o ambas ecuaciones multiplicándolas por los factores necesarios para que los coeficientes de una de las incógnitas sean iguales (pero de signo contrario).
2. Sumar o restar las ecuaciones. Combina las ecuaciones sumando o restando para eliminar una de las incógnitas, obteniendo así una nueva ecuación con una sola incógnita.
3. Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda.
4. Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones originales para encontrar el valor de la otra incógnita.

Ejemplo:

Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.

Sitema:

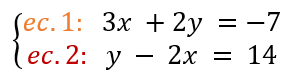
Seguimos las reglas:

1. Multiplicar para igualar coeficientes. Ajusta una o ambas ecuaciones multiplicándolas por los factores necesarios para que los coeficientes (los números que multiplican con las letras) de una de las incógnitas sean iguales (pero de signo contrario). Para más facilidad, ordenemos las ecuaciones.

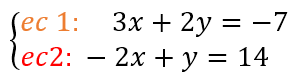
Ahora, escogemos eliminar una de las incógnitas. En nuestro ejemplo, escogeremos eliminar “y”. Para ello, debemos lograr que los coeficientes que acompañan a “y” en cada ecuación sean iguales, pero de signos contrarios. El la primera ecuación, el coeficiente que acompaña a “y” es 2, y en la segunda ecuación, el coeficiente que acompaña a “y” es 1. Debemos multiplicar un valor al coeficiente 2 de la primera ecuación, y otro valor al coeficiente 1 de la segunda ecuación para lograr que sean iguales con signos contrarios. ¿Qué valores usarías?

Por ejemplo, a 2 de la primera ecuación podría multiplicarlo por 3, entonces 2x3=6.

Entonces, a 1 de la segunda ecuación debería multiplicarlo por -6, entonces 1x(-6)=-6

Como puedes ver, ahora logramos que tengan el mismo valor, pero con signos contrarios. En nuestro ejemplo, logramos obtener 6 y -6.

Entonces, el valor que debemos multiplicar a la primera ecuación es 3 y a la segunda ecuación es -6. De esta forma los coeficientes de la incógnita “y” que queremos eliminar serán iguales pero de signo contrario, 6 y -6. Al multiplicar los valores por cada ecuación, aplicaremos la propiedad distributiva (no olvidemos la ley de signos):

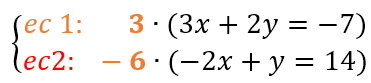
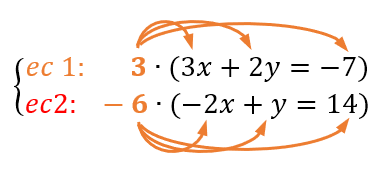
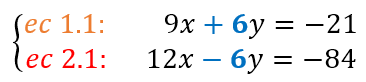
1. Sumar o restar las ecuaciones. Combina las ecuaciones sumando o restando para eliminar una de las incógnitas, obteniendo así una nueva ecuación con una sola incógnita. En nuestro ejemplo, sumamos “x” con “x”, y al operar “y” con “y”, esta se elimina debido a que sus coeficientes se neutralizan. También debemos sumar los valores del otro lado de las ecuaciones. Así:

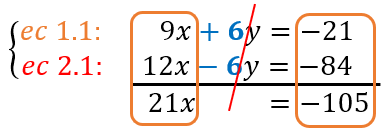
1. Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda. Como puedes ver, la nueva ecuación obtenida (ec. 3) es:

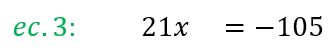
Al despejar “x” obtenemos:

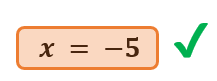
1. Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones originales para encontrar el valor de la otra incógnita. Para nuestro ejemplo, sustituiremos el valor de “x=-5” en la ecuación 1:

¡Y listo!

Podemos presentar la solución como un conjunto:

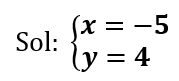
Ejercicios propuestos:

Solucionar los siguientes sistemas de ecuaciones por el método de reducción.

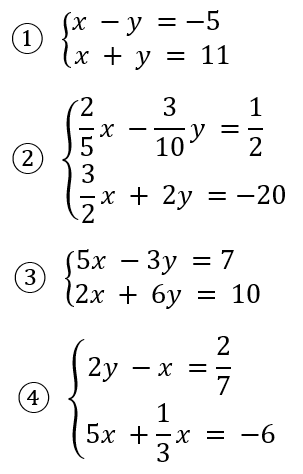
Soluciones:

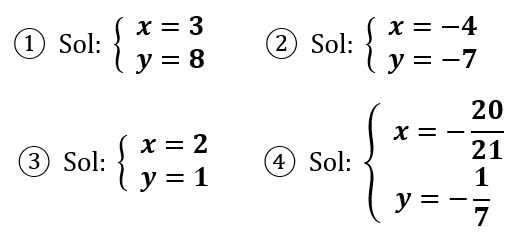
Aplicaciones

actividades

recursos adicionales