Método de sustitución

---

Imagina que tienes un rompecabezas complejo frente a ti, y la clave para resolverlo reside en encontrar el valor exacto de varias piezas interconectadas. Esto es similar a lo que enfrentamos en un sistema de ecuaciones lineales: un conjunto de ecuaciones que deben resolverse simultáneamente. El método de sustitución es como un camino secreto que te lleva paso a paso hacia la solución. Este método convierte una de las ecuaciones en una herramienta poderosa, sustituyendo variables y simplificando el sistema hasta que todo encaje perfectamente. Es una técnica esencial que no solo afila tus habilidades matemáticas, sino que también expande tu capacidad para resolver problemas complejos de manera estratégica y lógica.

Learning Goals

1. Comprender el Concepto del Método de Sustitución: Familiarizarse con la lógica detrás del método de sustitución y su aplicación en la resolución de sistemas de ecuaciones lineales.
2. Desarrollar Habilidades de Resolución: Aprender a aislar una variable en una de las ecuaciones del sistema y usar esa expresión para sustituirla en las demás ecuaciones.
3. Simplificación de Ecuaciones: Mejorar las habilidades para simplificar ecuaciones lineales, facilitando la resolución progresiva del sistema.
4. Resolución Paso a Paso: Seguir un proceso metódico y ordenado para resolver sistemas de ecuaciones lineales, verificando cada paso para garantizar la exactitud de la solución.
5. Aplicación Práctica: Aplicar el método de sustitución a problemas del mundo real, demostrando su utilidad en diversas disciplinas como la física, la economía y la ingeniería.

---

CONTENIDO

Reglas

Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.

Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.

Para el Método de Sustitución, procederemos así:

1. Escogemos una ecuación y una incógnita.
2. Despejamos esa incógnita de la ecuación escogida (es decir, la dejamos sola de un lado de la ecuación)
3. Reemplazamos la expresión despejada de esta incógnita en la misma incógnita pero de la otra ecuación (de esta manera, obtendremos una ecuación con una sola incógnita)
4. Despejamos esa incógnita y obtendremos su valor. Ya tenemos el valor de una de ellas.
5. Colocamos el valor obtenido de esta incógnita en cualquier otra ecuación, la despejamos y obtenemos el valor de la otra incógnita.

Ejemplo:

Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.

Sitema:

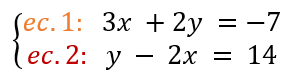
Seguimos las reglas:

1. Escogemos una ecuación y una incógnita. Escogeré, por ejemplo, la ecuación 1 (ec. 1), y de ella la incógnita “y“.

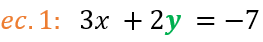
1. Despejamos esa incógnita de la ecuación escogida (es decir, la dejamos sola de un lado de la ecuación). Siguiendo el procedimiento de despeje de ecuaciones, al despajar “y” obtenemos una nueva ecuación (ec. 1.1) así:

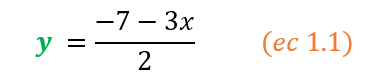
1. Reemplazamos la expresión despejada de esta incógnita “y” (de la ec. 1.1) en la misma incógnita “y“ pero de la otra ecuación del sistema (ec. 2). De esta manera, obtendremos una nueva ecuación (ec. 2.1) con una sola incógnita, la incógnita “x”. Veámoslo así:

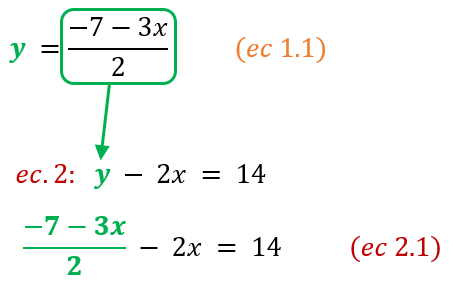
1. Despejamos esa incógnita “x” y obtendremos su valor. Con ello, ya tendríamos el valor de una de ellas, en este caso, de “x”.

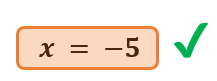
1. Colocamos el valor obtenido de esta incógnita “x” en cualquier otra ecuación, por ejemplo, en la ecuación “ec. 1.1”, con la cual, al efectuar los cálculos respectivos, obtenemos el valor de la otra incógnita.

¡Y listo!

Podemos presentar la solución como un conjunto:

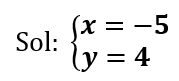
Ejercicios propuestos:

Solucionar los siguientes sistemas de ecuaciones por el método de sustitución.

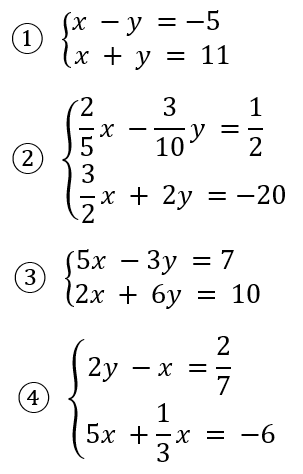
Soluciones:

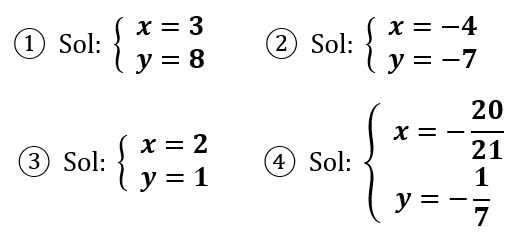
Aplicaciones

actividades

recursos adicionales