Método gráfico

---

¡Imagina que eres un artista matemático! Con el método gráfico, resolver sistemas de ecuaciones lineales se convierte en una experiencia visual y creativa. Piensa en cada ecuación como una línea en un gráfico, y tu misión es encontrar el punto exacto donde se cruzan. Ese punto es la solución a tu sistema. Es como unir piezas de un rompecabezas en el plano cartesiano. ¿Estás listo para descubrir cómo las matemáticas pueden ser tan visuales y divertidas como pintar un cuadro? 🎨📊

¿Te gustaría aprender más sobre cómo usar este método?

Learning Goals

1. Visualizar intersecciones: Aprender a representar ecuaciones lineales en un gráfico y encontrar el punto de intersección que representa la solución del sistema.
2. Comprender la geometría: Entender cómo las ecuaciones lineales se traducen en líneas rectas en el plano cartesiano y cómo sus intersecciones reflejan soluciones.
3. Interpretar gráficos: Desarrollar la habilidad de interpretar y analizar gráficos para determinar si un sistema tiene una solución única, múltiples soluciones o ninguna.
4. Aplicar en contextos reales: Utilizar el método gráfico para resolver problemas prácticos y cotidianos que pueden modelarse con sistemas de ecuaciones lineales.
5. Comparar métodos: Comparar el método gráfico con otros métodos de resolución (como sustitución y reducción) para evaluar cuándo es más eficiente y fácil de usar.

---

CONTENIDO

Reglas

Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada incógnita.

Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.

Para el Método Gráfico, procederemos así:

1. Dibujar las gráficas de las ecuaciones: Traza cada una de las ecuaciones en el mismo plano cartesiano. Dibuja las líneas rectas correspondientes usando sus pendientes e intersecciones con el eje “y”.
2. Encontrar el punto de intersección: Observa el gráfico para identificar el punto donde las dos líneas se cruzan. Este punto de intersección es la solución del sistema, donde ambos valores de “x” y “y” satisfacen ambas ecuaciones.

Ejemplo:

Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.

Sitema:

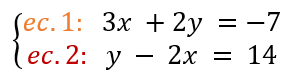
Seguimos las reglas:

1. Dibujar las gráficas de las ecuaciones: Traza cada una de las ecuaciones en el mismo plano cartesiano. Dibuja las líneas rectas correspondientes usando sus pendientes e intersecciones con el eje “y”.

Para graficar cada ecuación en el plano cartesiano, basta con obtener dos puntos de cada una, y luego trazar una recta que pase por ambos puntos. Para cada ecuación, los puntos se pueden obtener realizando una pequeña tabla de valores con dos valores.

Nota: Una forma rápida de obtener los puntos es igualar el valor de 0 en “x” y despejar “y”, y con eso obtendremos el primer punto. Luego, igualamos el valor de 0 en “y” y despejar “x”, y con eso obtendremos el segundo punto.

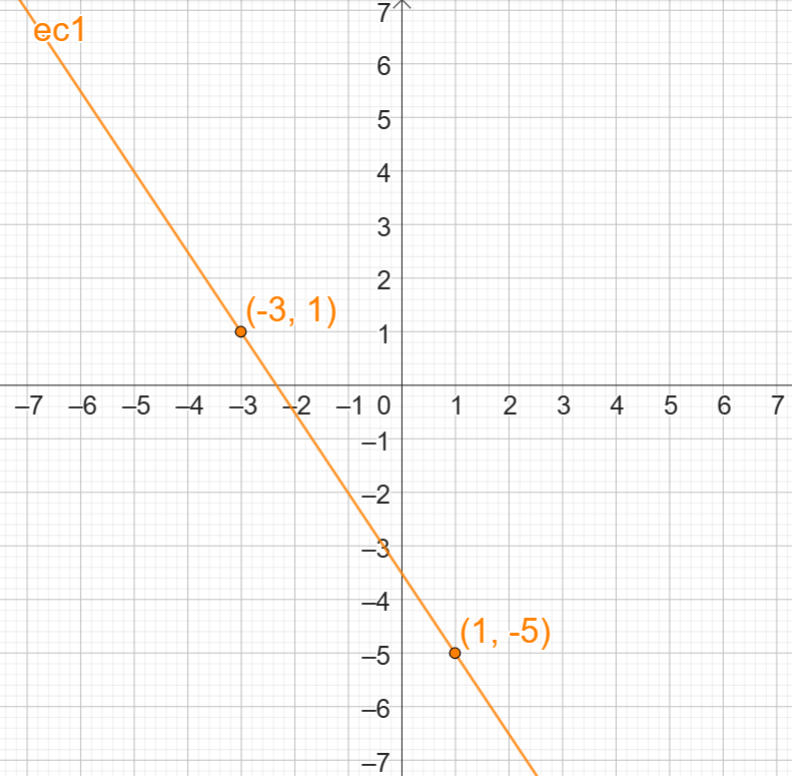
Para graficar la primera ecuación de nuestro ejemplo, construimos la tabla de valores respectiva (con dos valores solamente), los colocamos en el plano cartesiano y trazamos la recta respectiva que pase por ambos, así:

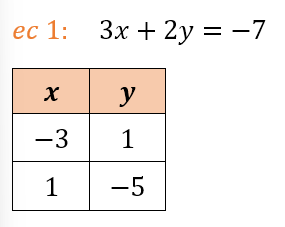
Procedemos de la misma forma para graficar la ecuación 2:

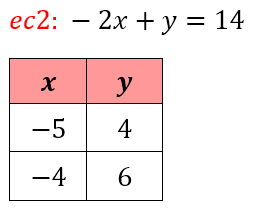
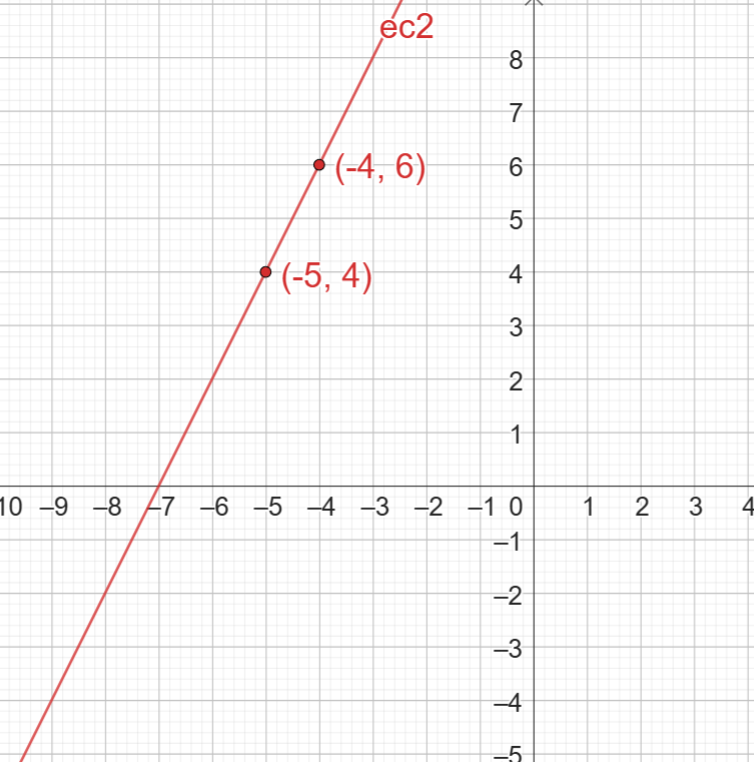
Las gráficas, vistas en un mismo plano, quedarían:

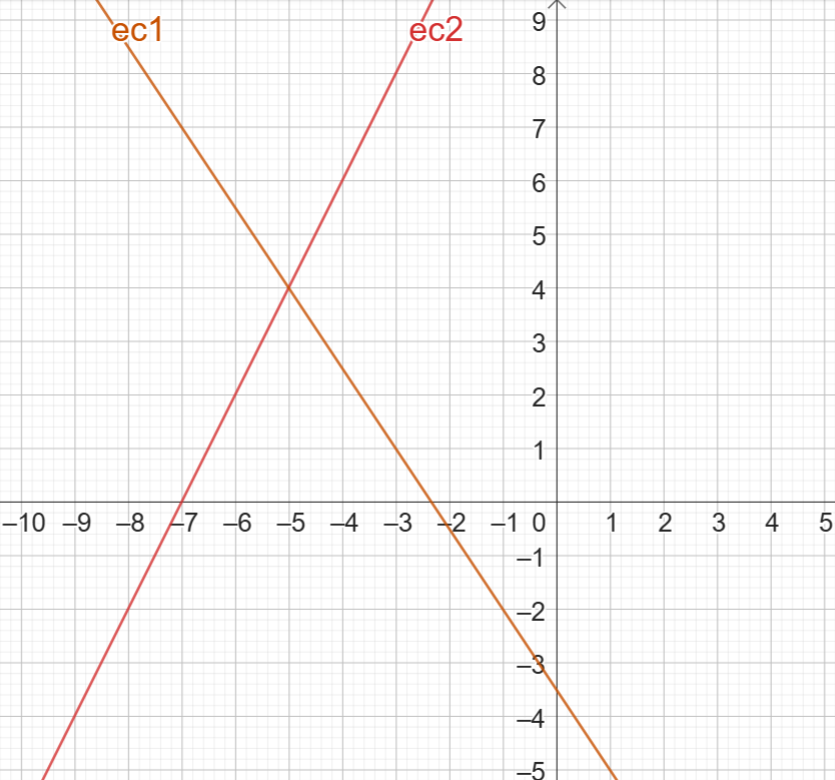
1. Encontrar el punto de intersección: Determinamos las coordenadas del punto en el que se cruzan. Así, en la gráfica podemos observar que el punto en el que se cruzan, tiene como coordenada “x” el valor de -5, y como coordenada “y” el valor de 4:

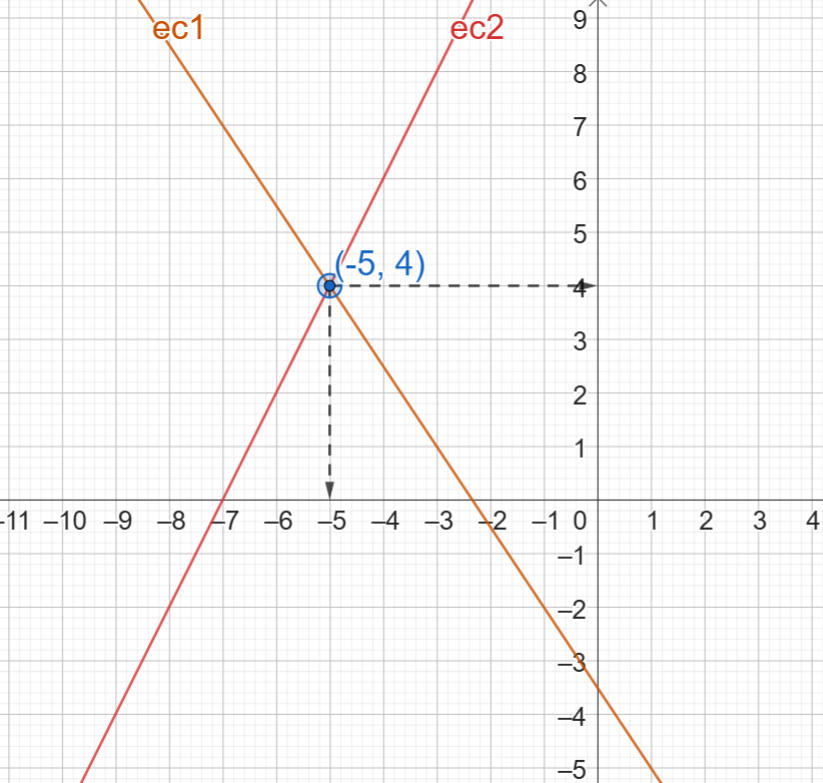
¡Y listo!

Podemos presentar la solución como un conjunto:

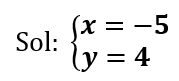
Ejercicios propuestos:

Solucionar los siguientes sistemas de ecuaciones por el método de reducción.

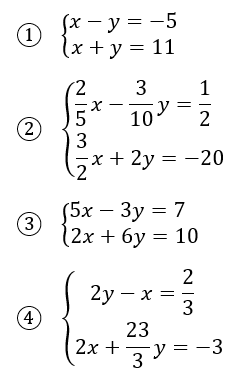
Soluciones:

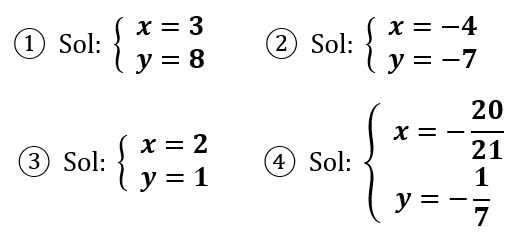
Aplicaciones

actividades

recursos adicionales