
¿Te imaginas tener una herramienta matemática que te permita resolver sistemas de ecuaciones de manera eficiente y precisa, como si estuvieras descifrando un código?
La Regla de Cramer es precisamente eso: un método poderoso que te permite encontrar soluciones a sistemas de ecuaciones lineales usando determinantes.
En esta lección, descubrirás cómo aplicar esta regla para resolver problemas complejos de manera simple y directa. Prepárate para desbloquear una nueva forma de entender y resolver ecuaciones, una habilidad que te será útil tanto en matemáticas como en situaciones prácticas del mundo real.
Learning goals
- Comprender el concepto de determinante y su relación con la Regla de Cramer.
- Aplicar la Regla de Cramer para resolver sistemas de ecuaciones lineales de manera eficiente.
- Desarrollar la habilidad para calcular determinantes de matrices y utilizarlos en la solución de problemas.
- Analizar situaciones del mundo real donde la Regla de Cramer es aplicable.
- Demostrar la capacidad para resolver problemas matemáticos utilizando la Regla de Cramer.
Contenido
Determinantes
Regla de Cramer
Ejercicios propuestos:
Resuelve los siguientes sistemas de ecuaciones por la Regla de Cramer (determinantes):
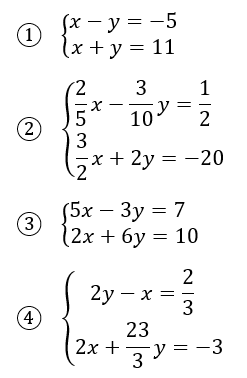
Soluciones:
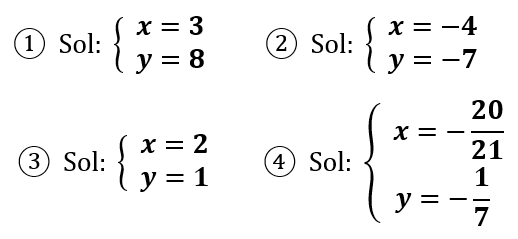
Actividades
- Competencia de Determinantes: Organiza una competencia donde los estudiantes calculen determinantes de matrices lo más rápido posible. Los más rápidos y correctos ganan puntos.
- Batalla de Cramer: Divide a los estudiantes en equipos, cada equipo debe resolver un sistema de ecuaciones utilizando la Regla de Cramer. El equipo que lo resuelva correctamente más rápido gana.
- Desafío de Ecuaciones: Crea un conjunto de problemas que requieren la aplicación de la Regla de Cramer. Los estudiantes deberán resolver tantos problemas como puedan dentro de un tiempo limitado. Los que resuelvan más problemas correctamente ganan.
- Caza de Tesoros Matemática: Diseña un juego donde los estudiantes deben resolver pistas matemáticas que involucran la Regla de Cramer para encontrar un “tesoro” oculto. Cada pista correcta los lleva al siguiente nivel.
- Escape Room Matemático: Crea un escape room virtual donde los estudiantes deben resolver sistemas de ecuaciones utilizando la Regla de Cramer para avanzar y “escapar” de la habitación. El equipo que lo haga más rápido gana.
Recursos adicionales
Enlaces:
- Khan Academy: Cramer’s Rule
- YouTube: Understanding Cramer’s Rule
- Desmos: Matrix and Determinant Calculator
- Wolfram Alpha: Cramer’s Rule Solver
- Interactive Tool for Solving Systems
Aplicaciones del mundo real

- Ingeniería Estructural: En la ingeniería civil, la Regla de Cramer se utiliza para calcular las fuerzas en los elementos de una estructura, asegurando su estabilidad y seguridad.
- Economía: Los economistas aplican la Regla de Cramer para resolver modelos económicos lineales que predicen la interacción de múltiples variables, como la oferta y la demanda en diferentes mercados.
- Redes Eléctricas: Los ingenieros eléctricos utilizan la Regla de Cramer para analizar circuitos y determinar corrientes y tensiones en redes complejas.
- Optimización de Recursos: En la gestión de proyectos, la Regla de Cramer se emplea para asignar recursos de manera óptima, resolviendo sistemas que incluyen múltiples restricciones.
- Criptografía: La Regla de Cramer es utilizada en la criptografía para descifrar códigos y en la teoría de números, donde los sistemas lineales juegan un papel fundamental.
Conclusiones
Este contenido te guiará en el aprendizaje de la Regla de Cramer, permitiéndote dominar una herramienta matemática esencial para resolver sistemas de ecuaciones de manera eficiente. ¡Prepárate para aplicar este conocimiento en contextos del mundo real y en desafíos matemáticos avanzados!
