Sistema de inecuaciones lineales (de una variable) y gráficas

Las inecuaciones son herramientas matemáticas fundamentales que nos permiten comparar expresiones y encontrar conjuntos de soluciones que satisfacen ciertas condiciones. A diferencia de las ecuaciones, donde buscamos un valor específico, en las inecuaciones buscamos rangos de valores que cumplen con una desigualdad. Descubrirás cómo estas poderosas expresiones pueden aplicarse en diversos campos, desde la economía hasta la ingeniería, y cómo proporcionan una base sólida para el razonamiento lógico y el análisis crítico. ¡Prepárate para explorar un mundo donde las soluciones no son únicas, sino infinitas!.
Learning Goals
- Identificar y comprender ecuaciones lineales: Reconocer la estructura de una ecuación lineal de una incógnita y entender sus componentes, como coeficientes y términos constantes.
- Resolver ecuaciones lineales de una incógnita: Aprender y practicar métodos para resolver ecuaciones lineales, incluyendo el despeje de la incógnita y la verificación de la solución.
- Aplicar ecuaciones lineales en problemas prácticos: Utilizar ecuaciones lineales para modelar y resolver situaciones cotidianas y problemas matemáticos, como encontrar precios, calcular distancias y determinar cantidades.
- Interpretar soluciones: Desarrollar la habilidad para interpretar la solución de una ecuación lineal en el contexto de un problema y comprender su significado en escenarios reales.
- Comunicar procesos y soluciones: Presentar y explicar los pasos seguidos para resolver ecuaciones lineales y las soluciones obtenidas, utilizando un lenguaje matemático claro y preciso.
CONTENIDO
Elementos de la inecuación
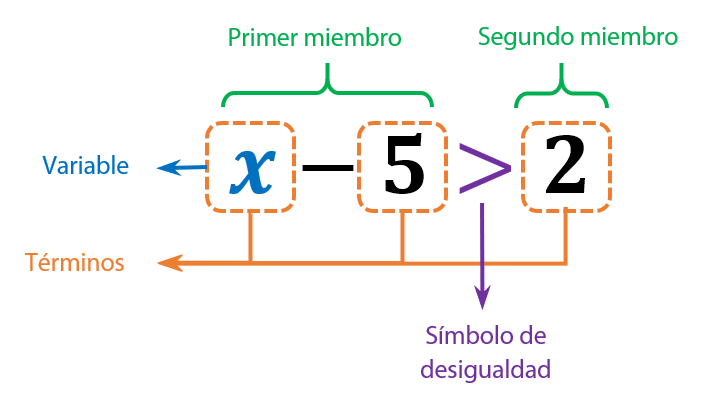
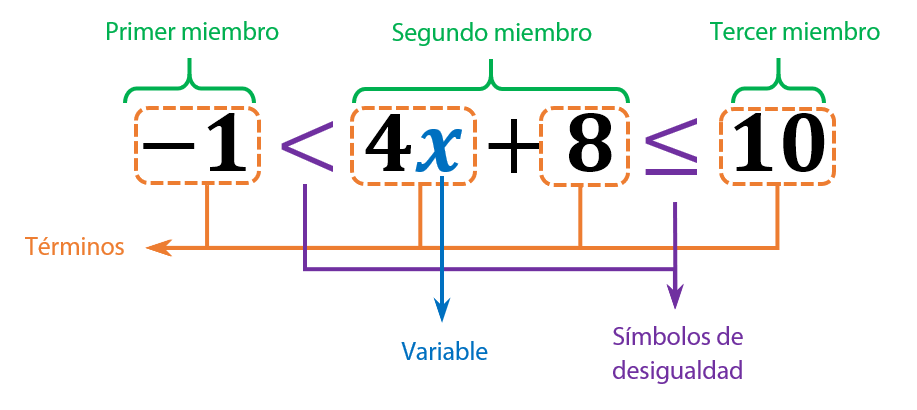
Miembros: En una inecuación, los miembros son las dos expresiones que se encuentran a cada lado del símbolo de la inecuación. Por ejemplo, en la inecuación 2x+3>5, los miembros son, el de la izquierda (primer miembro) 2x+3, y el de la derecha (segundo miembro) 5.
Términos: Los términos son los elementos individuales que componen los miembros de la inecuación, separados los los símbolos de suma (+) y resta (-). Estos pueden ser números, variables o productos de números y variables. En la inecuación 2x+3>5, los términos son 2x y 3 en el primer miembro, y 5 en el segundo miembro.
Variable: La variable es el símbolo que representa un valor desconocido que queremos determinar. En las inecuaciones, las variables suelen ser letras como x, y, z, etc. En la inecuación 2x+3>5, la variable es x.
Símbolo de la inecuación: El símbolo de la inecuación es el signo que indica la relación de desigualdad entre los dos miembros de la inecuación. Los símbolos más comunes son:
- >: mayor que
- ≥: mayor o igual que
- <: menor que
- ≤: menor o igual que
Por ejemplo, en la inecuación 2x+3>5, el símbolo > indica que el primer miembro es mayor que el segundo miembro.
Intervalos
La solución de una inecuación se presenta como un intervalo, y no como solución única. Lo explicaremos mejor: una solución única es aquella que determina un único valor para una incógnita. Por ejemplo, x=2 indica que “x” vale 2 y no otro valor, tal y como sucedió en el tema de ecuaciones. Por otro lado, en las inecuaciones, un intervalo es un rango de valores que puede tomar una incógnita (a la que llamaremos variable porque puede variar en su valor) desde un “inicio” hasta un “fin”, de tal manera que los valores en ese rango cumplan con lo indicado con la inecuación. Por ejemplo, [3, 5] indica que “x” puede tomar cualquier valor desde el 3 hasta el 5, incluyendo números decimales. No te preocupes por la notación que acabas de leer. Lo explicaremos a continuación.
Notación de intervalos
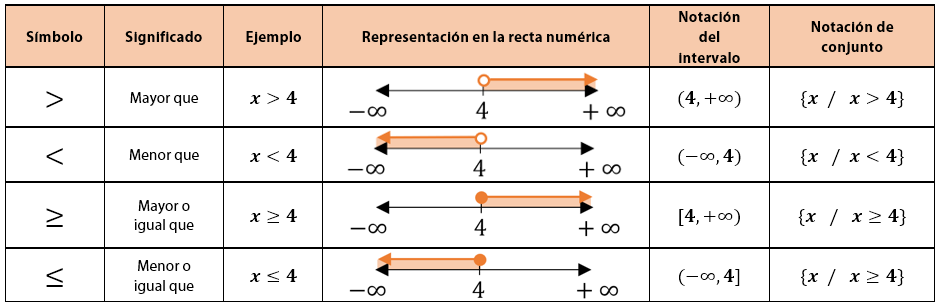
Antes de pasar a la representación de intervalos en la variedad de sus notaciones, te explicaremos qué significan los símbolos utilizados, en la tabla a continuación:

Nota: los infinitos siempre son abiertos.
Por ejemplo:
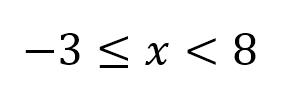
En el ejemplo, la solución de “x” está entre los valores que van desde -3 hasta 8, pero con las siguientes consideraciones:
- -3 está incluido en la solución, puesto que el símbolo que lo acompaña es ≤, le corresponde un corchete cerrado, “comiendo” al número -3, y en representación gráfica le corresponde un punto pintado ●.
- 8 está excluido de la solución, puesto que el símbolo que lo acompaña es <, le corresponde un corchete abierto, “dándole la espalda” al número 8, y en representación gráfica le corresponde un punto despintado ◯.
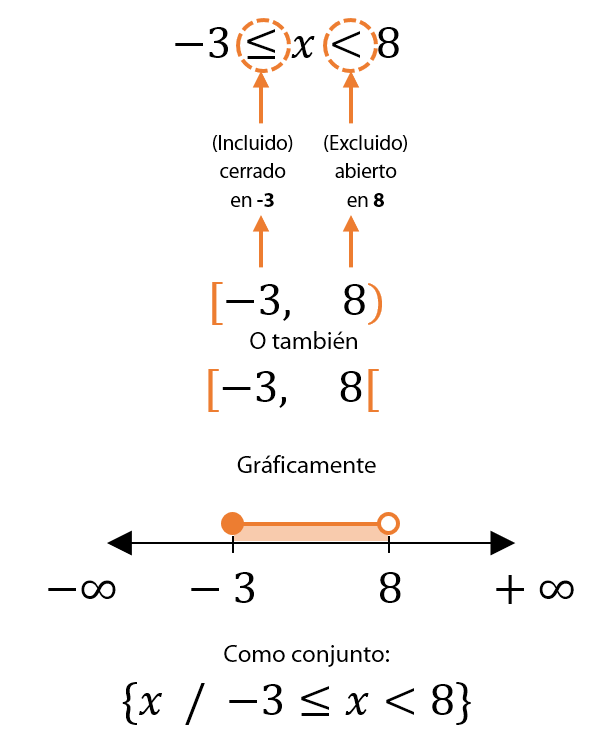
Otros ejemplos:
Resolución de inecuaciones lineales de una incógnita
Debemos seguir las siguientes reglas:
Reglas sencillas para resolver inecuaciones lineales
- Suma y Resta:
- Si suma, pásalo al otro lado restando, pero NO cambies el signo de la desigualdad.
- Si resta, pásalo al otro lado sumando, pero NO cambies el signo de la desigualdad.
- Multiplicación y División por Número Positivo:
- Si multiplica o divide por un número positivo, pásalo al otro lado con la operación contraria, pero NO cambies el signo de la desigualdad.
- Multiplicación y División por Número Negativo:
- Si multiplica o divide por un número positivo, pásalo al otro lado con la operación contraria, e INVIERTE el signo de la desigualdad.
Ejemplo 1:
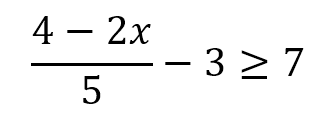
Pasamos el -3, que está restando, a sumar al otro lado. Recuera que NO cambia el símbolo de la inecuación.
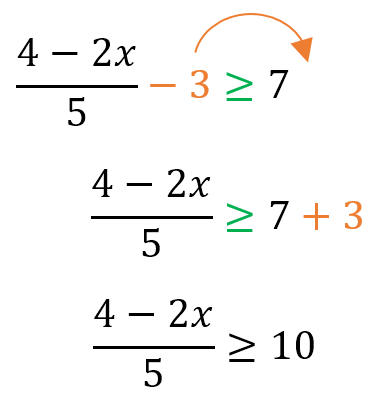
Ahora, fíjate que el 5 está dividiendo a todo lo que está arriba, por lo tanto, pasa al otro lado a multiplicar. Como el 5 es positivo, NO cambia el símbolo de la inecuación.
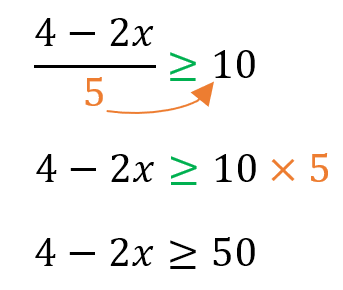
A continuación, el 4, aunque parezca que está restando con 2x, por su signo positivo se considera que está “sumando” a -2x, por lo que pasa con signo contrario al otro lado, y el símbolo de la inecuación NO cambia. Así:
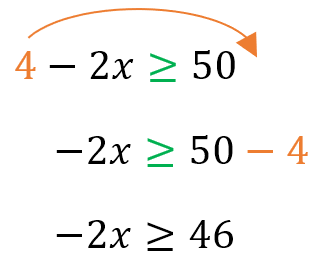
Ahora, le toca el turno a -2, que está multiplicando por x. Debe pasar a dividir al otro lado, pero al ser un número negativo, INVIERTE el símbolo de la inecuación, así:
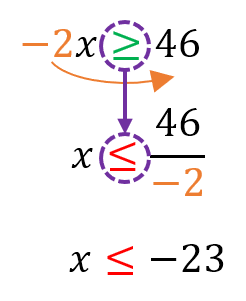
Por lo tanto, la solución del ejercicio comprende a todo valor menor o igual a -23.
Representándolo en la recta numérica, queda así:
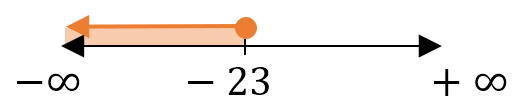
Representándolo como intervalo queda:
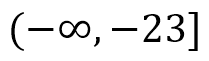
O también:
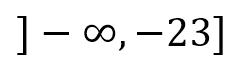
Finalmente, podemos expresarlo como notación de conjunto, así:
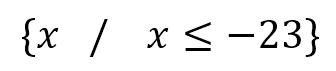
Ejemplo 2:
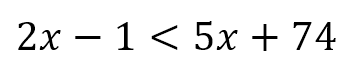
En este ejemplo, vemos que “x” se encuentra a ambos lados de la inecuación. Pasamos primero las “x” a un solo lado, y los términos que no contienen “x” del otro lado (recordemos que como están haciendo operaciones de suma o resta, deben pasar con signo contrario), y NO cambia el símbolo de la desigualdad. Así:
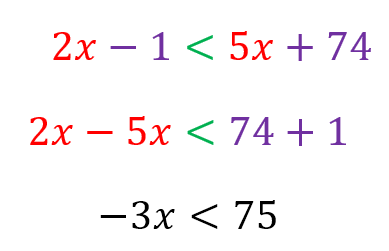
Luego, -3 pasa a dividir, conservando su signo negativo, pero INVIRTIENDO el símbolo de la inecuación. Así:
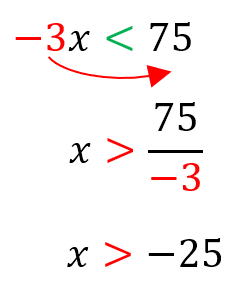
Representándolo en la recta numérica, queda así:
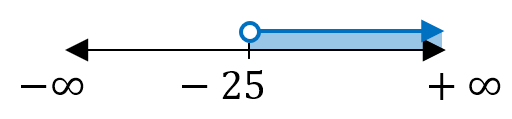
Representándolo como intervalo queda:
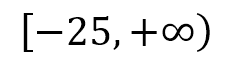
O también:
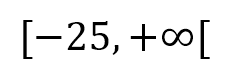
Finalmente, podemos expresarlo como notación de conjunto, así:
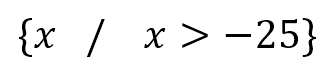
Resolución de sistemas de inecuaciones lineales de una sola incógnita
Un sistema de inecuaciones lineales comprende a un conjunto de estos, cuya solución es la intersección de las soluciones.

Ejemplo:
Para nuestro ejemplo, tomaremos los ejercicios de ejemplo anteriores para armar nuestro sistema de inecuaciones:
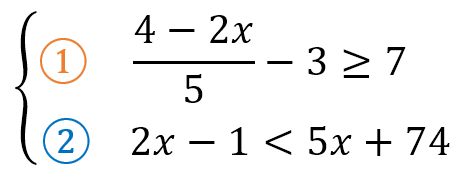
Y dado que ya los habíamos resuelto anteriormente en los ejemplos, sabemos que la soluciones son:
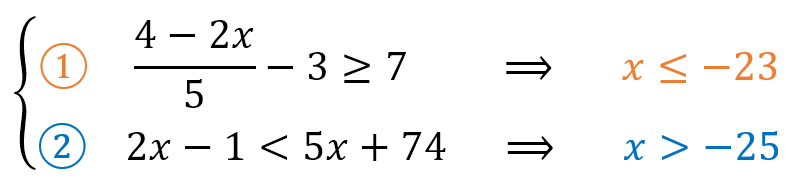
Recordemos también que sus soluciones gráficas son:

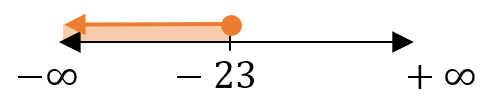

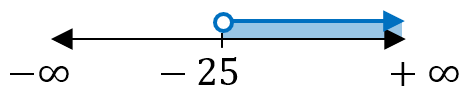
Unimos las soluciones de ambas inecuaciones en la misma recta numérica:
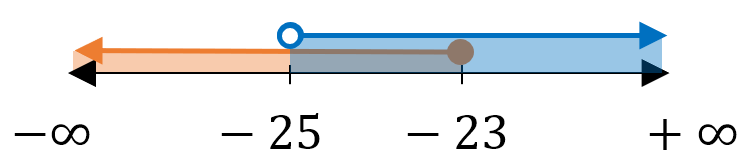
El conjunto solución corresponde a la región en donde se intersecan o “cruzan”:
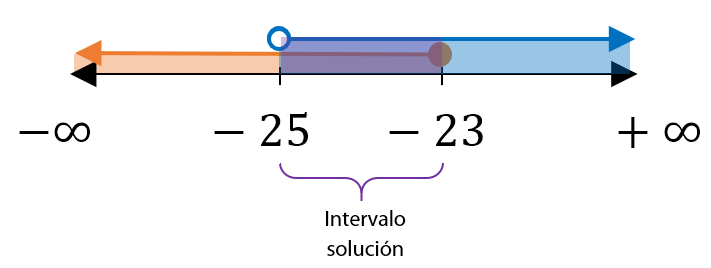
Cómo puedes observar, el intervalo solución, en donde se cruzan las soluciones individuales de cada inecuación, es el que va desde -25 (abierto o excluido) hasta -23 (cerrado o incluido):
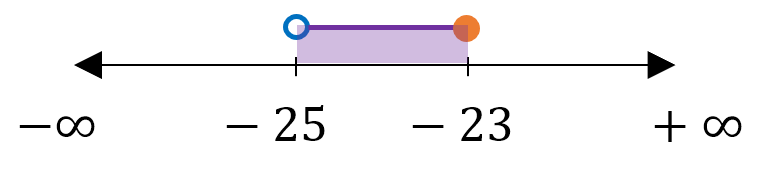
Escrito en forma de intervalo, queda:
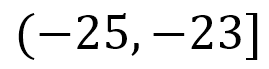
O también:
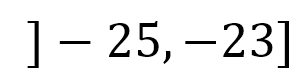
En forma de conjunto solución, queda:
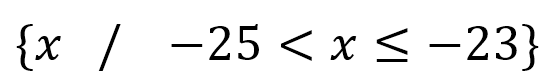
Aplicaciones

Planificación de gastos:
- Quieres controlar cuánto puedes gastar en entretenimiento, como ir al cine o salir a cenar, sin pasarte del presupuesto que te has fijado.
Control de dieta:
- Estás siguiendo una dieta y necesitas saber cuántas meriendas saludables puedes comer al día sin exceder tu límite de calorías.
Ahorros para una compra:
- Deseas ahorrar dinero para comprar algo específico, como un gadget, y necesitas saber cuánto tiempo te llevará juntar el dinero necesario ahorrando una cantidad fija cada semana.
