Las ecuaciones cuadrĆ”ticas, aunque pueden parecer abstractas, tienen aplicaciones fascinantes en la vida real. Desde la trayectoria de un balĆ³n de fĆŗtbol en un partido decisivo hasta la optimizaciĆ³n de recursos en un negocio, estas ecuaciones nos permiten resolver problemas cotidianos de manera eficiente. Ā”Descubre cĆ³mo esta poderosa herramienta matemĆ”tica impacta nuestro mundo de formas sorprendentes y prĆ”cticas! šš
Learning Goals
- Comprender el Concepto: ReconocerƔs y entenderƔs las ecuaciones cuadrƔticas y su estructura bƔsica.
- AplicaciĆ³n PrĆ”ctica: IdentificarĆ”s y resolverĆ”s problemas de la vida real que pueden ser modelados y resueltos usando ecuaciones cuadrĆ”ticas.
- AnƔlisis de Trayectorias: CalcularƔs la trayectoria de objetos en movimiento, como pelotas o proyectiles, usando ecuaciones cuadrƔticas.
- OptimizaciĆ³n de Recursos: AplicarĆ”s ecuaciones cuadrĆ”ticas para optimizar situaciones prĆ”cticas, como maximizar Ć”reas o minimizar costos.
- Desarrollo de Habilidades de ResoluciĆ³n: DesarrollarĆ”s habilidades para resolver ecuaciones cuadrĆ”ticas usando diferentes mĆ©todos, como factorizaciĆ³n, fĆ³rmula cuadrĆ”tica.
CONTENIDO
Ejercicios de aplicaciĆ³n
Los ejercicios que se muestran a continuaciĆ³n fueron tomados de las evaluaciones del Ineval para el acceso a la educaciĆ³n superior desde el aƱo 2017. Estos ejercicios permitirĆ”n aplicar los conocimientos adquiridos en las lecciones anteriores. Es importante que el estudiante reconozca los elementos de la funciĆ³n cuadrĆ”tica y los cĆ”lculos necesarios que se necesitan para contestar a las preguntas indicadas.
Ejercicio 1:
En un juego de vĆ³ley, la trayectoria de una pelota se expresa por š¦ = 2 + 4š„ ā š„2 ; donde y es la altura y x el desplazamiento. Determina la grĆ”fica que corresponde a esta trayectoria.
Opciones:
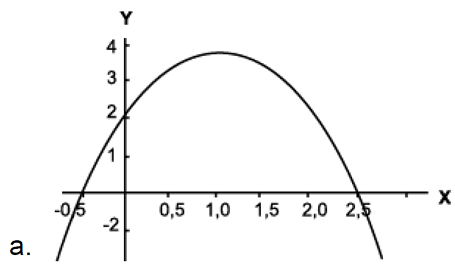
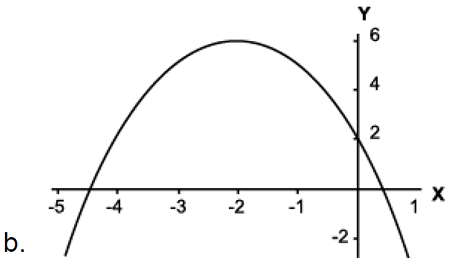
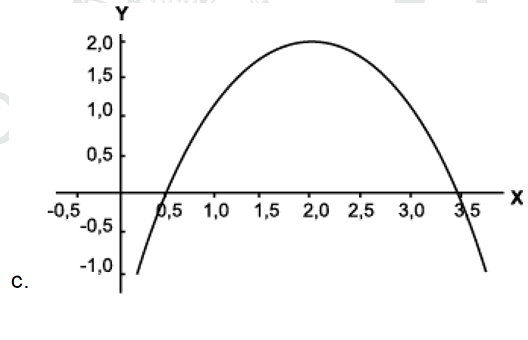
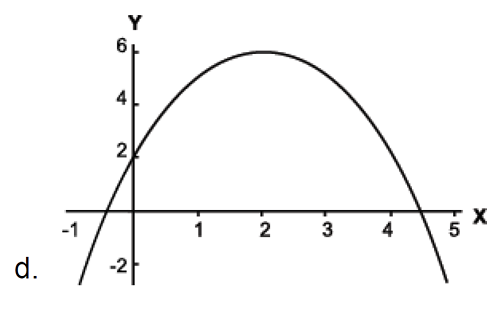
Ejercicio 2:
Un jugador realiza un pase de tal manera que el balĆ³n se aleja describiendo un movimiento parabĆ³lico dado por la ecuaciĆ³n:
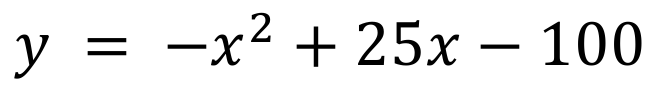
Determina la distancia a la que caerĆ” la pelota respecto del jugador. Considera que el campo de juego se encuentra sobre el eje de las abscisas.
Opciones:
a. 20,00
b. 56,25
c. 15,00
d. 12,50
Ejercicio 3:
Una cocina solar de forma parabĆ³lica se fabrica siguiendo la ecuaciĆ³n: š¦=š„2+14š„+48 y estĆ” montada sobre un mesĆ³n, cuyo borde coincide con el eje de las abscisas. Si todas las medidas estĆ”n dadas en metros, determina la profundidad que deberĆ” tener el mesĆ³n para que la cocina quepa perfectamente.
Opciones:
a. 0.8
b. 0.6
c. 1.0
d. 0.3
Ejercicio 4:
Un ingeniero elĆ©ctrico estĆ” instalando lĆ”mparas de iluminaciĆ³n externa en una bodega. Para hacerlo correctamente debe colocar la lĆ”mpara mĆ”s potente en el punto mĆ”s alto de la pared frontal, cuya parte superior tiene una forma parabĆ³lica. Con la ayuda de un topĆ³grafo se ha determinado la funciĆ³n que describe el perfil de la parte superior de la pared:
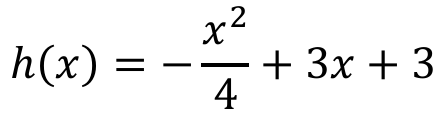
Donde h es la altura de la pared desde el piso y x es la distancia horizontal medida desde el lado izquierdo de la pared, todo en metros. Si la curvatura parabĆ³lica de la pared empieza a 3 metros de altura, Āæa quĆ© altura, desde el piso, en metros, se debe instalar la lĆ”mpara mĆ”s potente?
Opciones:
a. 9
b. 12
c. 15
d. 6
Ejercicio 5:
Un niƱo encuentra la pelota de su vecino en su patio, y para devolverla debe pasar un muro que separa las dos casas. La trayectoria que sigue la pelota se describe en la funciĆ³n descrita en la figura:
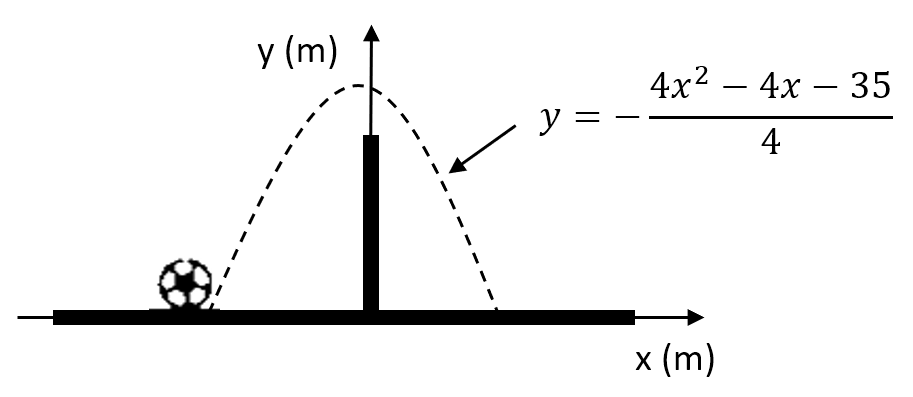
La pelota se encontraba a _______ metros a la izquierda del muro, y cayĆ³ a _______ metros a la derecha del muro.
Opciones:
a. 5/2, 7/2
b. 7/2, 5/2
c. 7/4, 5/4
d. 5/4, 7/4
Ejercicio 6:
Los ingresos de la sucursal de una empresa estƔn dirigidos en su totalidad para pagar toda la materia prima adquirida para su apertura, como se muestra en la figura:
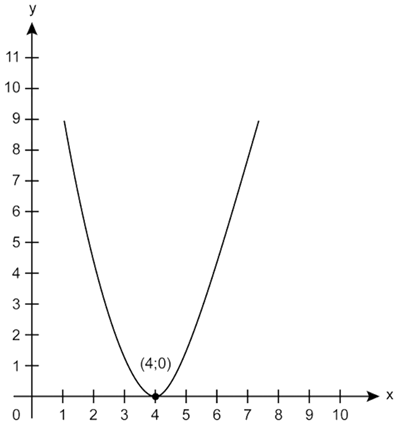
Determina el dominio de la funciĆ³n que muestra el crecimiento en los ingresos de la empresa, para tener un control presupuestario.
Opciones:
a. [0; ā+[
b. [4; ā+[
c. ]āā; 4]
d. ]āā; ā+[