Función cuadrática y gráficas

---

La función cuadrática es la clave para entender las curvas y trayectorias que encontramos en la vida diaria, desde el arco de una pelota hasta las órbitas planetarias. Con la simple fórmula y=ax²+bx+c, puedes desentrañar patrones ocultos y resolver problemas complejos. Sumérgete en el mundo de las parábolas y descubre cómo esta poderosa herramienta matemática puede transformar tu comprensión del universo. 📐✨🚀

Learning Goals

1. Identificar la forma estándar de una función cuadrática: Reconocer y escribir la función cuadrática en su forma estándar $$y = ax^2 + bx + c$$.
2. Comprender el papel del coeficiente cuadrático: Entender cómo el valor de “a” afecta la abertura y la dirección de la parábola.
3. Encontrar el vértice de la parábola: Aprender a calcular y ubicar el punto máximo o mínimo de la parábola, conocido como el vértice.
4. Determinar las raíces o soluciones: Saber cómo encontrar los valores de “x” donde la función cuadrática cruza el eje x.
5. Graficar la función cuadrática: Desarrollar la habilidad de trazar la parábola en un plano cartesiano utilizando puntos clave como el vértice y las raíces.

---

CONTENIDO

Función cuadrática

Una función cuadrática es de tipo polinomio de grado 2. Para explicarlo más claro, el mayor valor del exponente de la variable independiente “x” es 2, y su gráfica es una parábola.

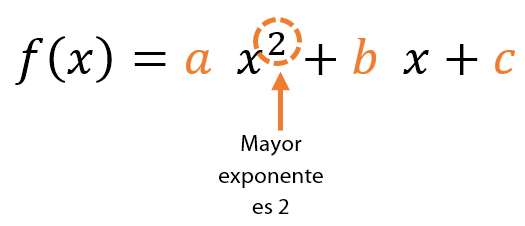
¿Qué es una parábola?

Una parábola es una gráfica de forma curva que va y viene una sola vez. En la función cuadrática, la parábola tiene un valor máximo si sube y luego baja; o mínimo si baja y luego sube (recordemos que las gráficas se leen de izquierda a derecha).

Coeficientes de la función cuadrática

Los coeficientes son los valores numéricos que acompañan a la variable independiente “x”.

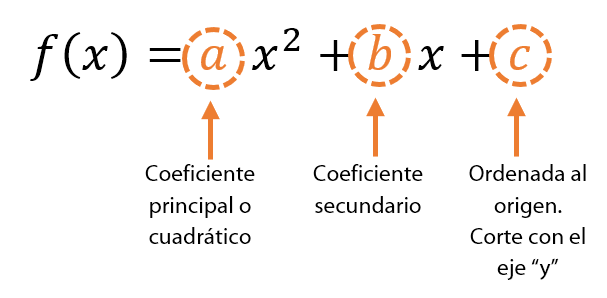
• a Coeficiente principal: es el que multiplica con x². Debe estar presente. Si es positivo, la parábola se abre hacia arriba (cóncava positiva), mas si es negativo, la parábola se abre hacia abajo (cóncava negativa).
• b Coeficiente secundario: es el que multiplica con x. Este puede o no estar presente.
• c Ordenada al origen: es el último término, va solo y no multiplica con x. Este puede o no estar presente. Indica en qué valor del eje “y” pasa exactamente la gráfica. Si no está presente, entonces su valor es cero (0) y significa que la gráfica pasa exactamente por el origen.

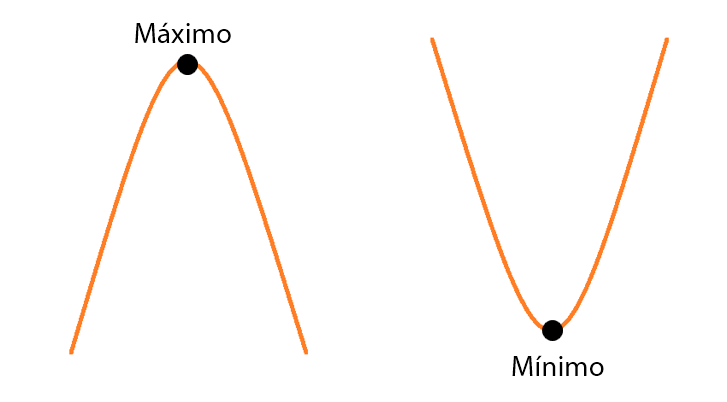
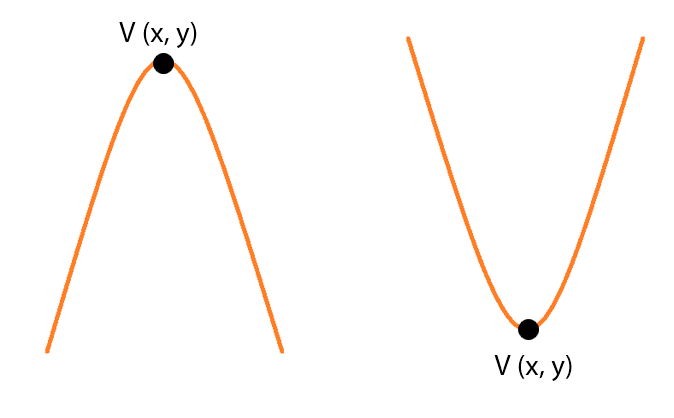
Vértice

Vértice es el punto (es decir, con coordenadas x, y) máximo o mínimo de la parábola.

Para hallar la coordenada en x del vértice, aplicamos la fórmula:

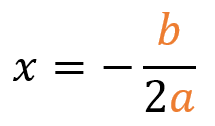
Para hallar la coordenada y del vértice, simplemente reemplazamos el valor obtenido de la fórmula anterior en la función, o también podemos aplicar su propia fórmula. es decir:

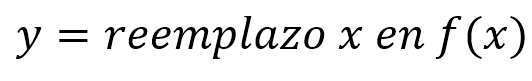
o

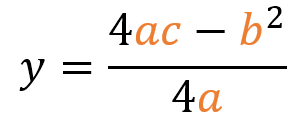
Ejemplo: Gráfica aproximada

Graficar la función:

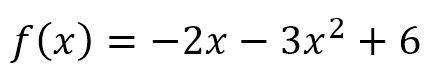
Aunque no es necesario, resulta más fácil ordenar los términos de la función, así:

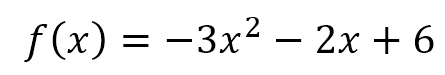
Luego, identificamos los coeficientes:

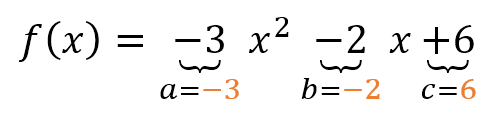
Interpretemos:

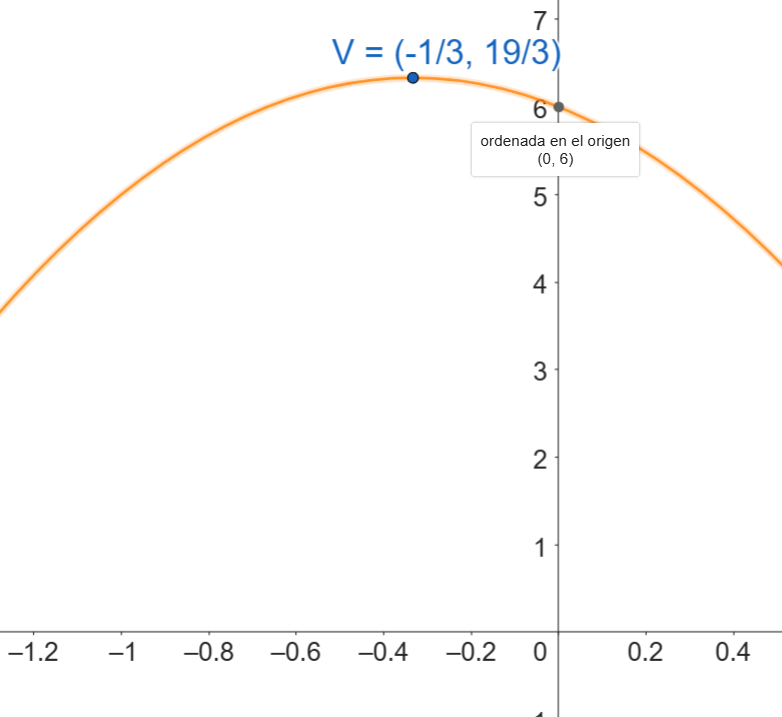
• a=-3, por ser negativa, la parábola es cóncava negativa, es decir, que se abre hacia abajo.
• c=6, que indica que la gráfica de la parábola cruza por el eje “y” en el valor 6.
• Calculamos el vértice:

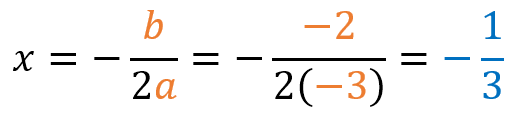
Para la coordenada “y” del vértice, podemos reemplazar el valor obtenido de x=-1/3, o aplicar la fórmula para “y”.

Reemplazando:

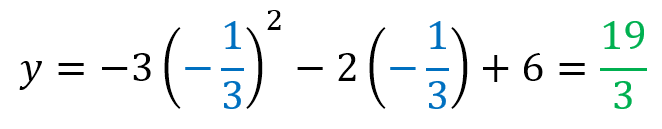
O usando la fórmula para “y”:

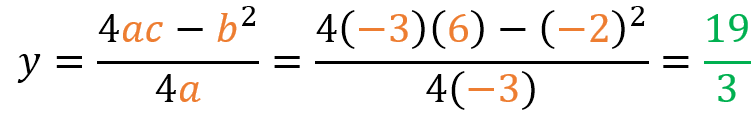
Por lo tanto, el vértice es:

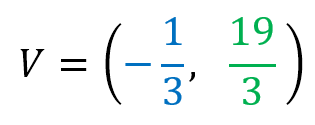
La gráfica aproximada de esta función es:

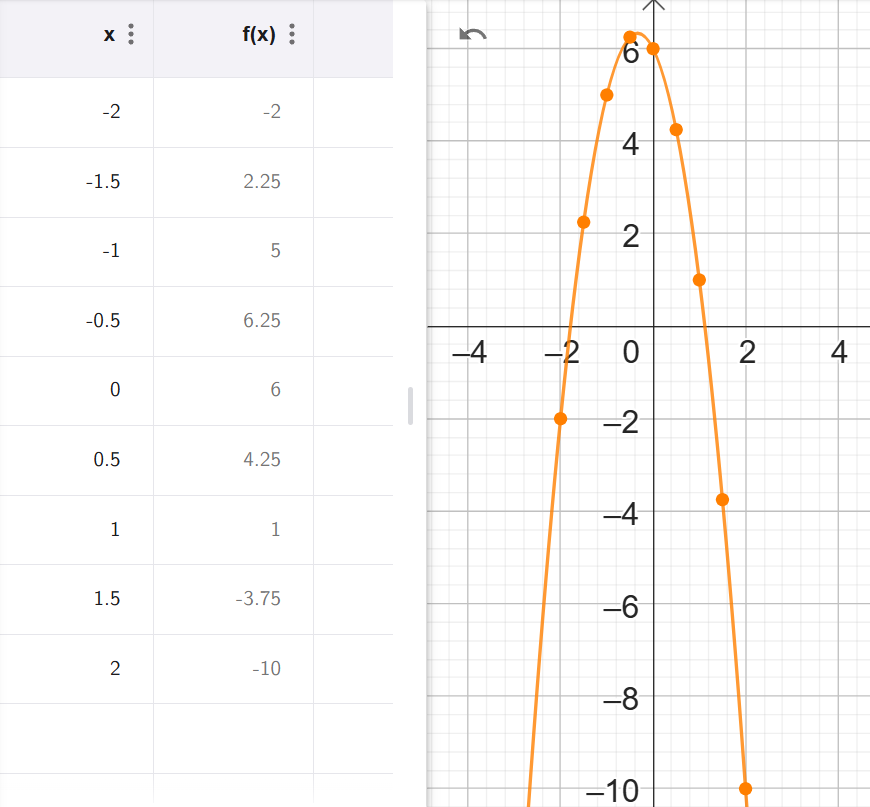
Gráfica con tabla de valores:

Para mayor precisión, podemos usar la tabla de valores para obtener la gráfica de la función.

Para ello, colocamos valores a x, y los reemplazamos en la función para obtener los correspondientes valores de y.

Dominio y rango de la función cuadrática:

Aplicaciones

actividades

recursos adicionales