Resolución de triángulos rectángulos: Teorema del cateto y Teorema de la altura.

¡Bienvenido a una nueva aventura matemática! ¿Sabías que los triángulos rectángulos tienen secretos fascinantes esperando a ser descubiertos? Con el Teorema del Cateto y el Teorema de la Altura, desvelarás cómo estas figuras pueden ayudarte a resolver problemas geométricos de manera ingeniosa. Estos teoremas son como herramientas mágicas que te permitirán encontrar longitudes y alturas sin necesidad de medirlas directamente. Prepárate para explorar cómo los matemáticos utilizan estas poderosas técnicas para simplificar cálculos y resolver desafíos del mundo real. ¡Vamos a sumergirnos en el emocionante mundo de los triángulos rectángulos y a descubrir cómo puedes convertirte en un maestro de la resolución geométrica!
Learning Goals
- Comprender el Teorema del Cateto: Aprenderás a enunciar y aplicar el Teorema del Cateto para encontrar la longitud de un cateto en un triángulo rectángulo.
- Comprender el Teorema de la Altura: Serás capaz de enunciar y aplicar el Teorema de la Altura para determinar la longitud de la altura en un triángulo rectángulo.
- Resolver triángulos rectángulos: Aprenderás a resolver triángulos rectángulos utilizando ambos teoremas para encontrar longitudes desconocidas de lados y alturas.
- Aplicar teoremas en problemas prácticos: Utilizarás los teoremas del cateto y de la altura para resolver problemas geométricos y situaciones del mundo real de manera precisa y eficaz.
- Visualizar triángulos rectángulos: Desarrollarás habilidades para dibujar y etiquetar triángulos rectángulos correctamente, representando las relaciones entre catetos, hipotenusa y altura de manera clara.
CONTENIDO
Fuente:
Teorema del cateto
En un triángulo rectángulo, el cuadrado de uno de los catetos es igual al producto de su proyección sobre la hipotenusa por la propia hipotenusa.
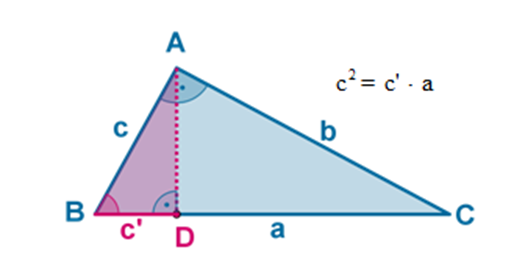
Puedes ver la demostración del teorema paso a paso en el siguiente applet.
Actividad 1
Lee y completa.
De ser necesario hacer una aproximación, redondea a las centésimas y separa la parte decimal del número con una coma:
Dado un triángulo rectángulo con hipotenusa de 17 cm.
- Si un cateto mide 8 cm, la proyección del mismo sobre la hipotenusa mide _____ cm.
- Si el otro cateto mide 15 cm, la proyección del mismo sobre la hipotenusa mide _____ cm.
Teorema de la altura
En un triángulo rectángulo, el cuadrado de la altura medida sobre la hipotenusa es igual al producto de las proyecciones de los dos catetos sobre la hipotenusa.
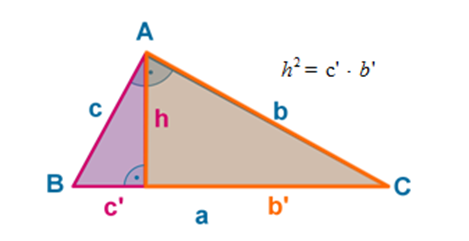
Demostración
Puedes ver la demostración del teorema paso a paso en el siguiente applet.
Actividad 2
Lee y completa.
De ser necesario hacer una aproximación, redondea a las centésimas y separa la parte decimal del número con una coma.
En un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa miden 3,5 cm y 14 cm.
Se puede deducir que la altura mide ____ cm.
Aplicaciones

Teorema del Cateto
- Diseño de Rampas 🛤️
- Descripción: Para construir una rampa accesible, puedes calcular la longitud necesaria de la rampa utilizando la altura del desnivel y la distancia horizontal que debe cubrir.
- Ejemplo: Determinar la longitud de una rampa para acceder a una entrada elevada a partir de la altura del escalón y la distancia horizontal disponible.
- Estructuras Triangulares ⛺
- Descripción: En el diseño de carpas y tiendas de campaña, se utilizan triángulos rectángulos. Usando el Teorema del Cateto, puedes calcular las longitudes necesarias de los soportes laterales.
- Ejemplo: Calcular la longitud de los laterales de una tienda de campaña sabiendo la altura y la base del triángulo.
- Proyectos de Carpintería 🪚
- Descripción: Los carpinteros usan el Teorema del Cateto para calcular la longitud de tablas y otros materiales en proyectos que involucran ángulos rectos.
- Ejemplo: Determinar la longitud de una tabla diagonal en un estante de esquina a partir de las longitudes de los lados del estante.
Teorema de la Altura
- Ajuste de Péndulos ⏳
- Descripción: Para ajustar un péndulo, es esencial conocer la relación entre la longitud del hilo y la altura desde la cual se cuelga. El Teorema de la Altura permite estos cálculos.
- Ejemplo: Calcular la longitud del hilo de un péndulo a partir de la altura y la distancia desde el punto de suspensión al péndulo.
- Arquitectura de Puentes 🌉
- Descripción: En el diseño de puentes colgantes, la altura y la longitud de los cables deben calcularse con precisión. El Teorema de la Altura ayuda a determinar estas dimensiones.
- Ejemplo: Determinar la longitud de los cables de un puente colgante a partir de la altura de las torres y la distancia entre ellas.
- Astrofísica y Observación Estelar 🌠
- Descripción: En la observación de estrellas, el Teorema de la Altura permite a los astrónomos calcular la altura de un cuerpo celeste en el cielo nocturno a partir de su ángulo de elevación y la distancia desde el observador.
- Ejemplo: Calcular la altura de una estrella sobre el horizonte utilizando el ángulo de observación y la distancia conocida.
