
Las medidas de tendencia central son fundamentales en estadística porque nos permiten resumir un conjunto de datos utilizando un único valor que representa el centro de la distribución. Estas medidas incluyen la media, la mediana y la moda.
En esta lección, aprenderemos a calcular cada una de estas medidas para datos no agrupados y entenderemos su importancia a través de ejemplos prácticos.
Learning Goals
- Calcular la media aritmética: Aprenderás a calcular la media aritmética (promedio) de un conjunto de datos no agrupados y entenderás cómo este valor representa el centro de los datos.
- Determinar la mediana: Serás capaz de identificar y calcular la mediana de un conjunto de datos no agrupados, comprendiendo su papel como el valor central que divide el conjunto de datos en dos partes iguales.
- Identificar la moda: Aprenderás a encontrar la moda de un conjunto de datos no agrupados y entenderás cómo este valor muestra la frecuencia del dato más común.
- Aplicar medidas de tendencia central: Podrás aplicar los conceptos de media, mediana y moda para analizar y resumir datos en diferentes situaciones prácticas, mejorando tu capacidad para interpretar información estadística.
CONTENIDO
Media
La media aritmética, o simplemente media, es el promedio de todos los valores en un conjunto de datos. Se calcula sumando todos los valores y dividiendo el resultado entre el número total de valores.
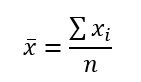
Ejemplo:
Supongamos que tenemos las siguientes edades de un grupo de estudiantes: 12, 14, 15, 13, 12.
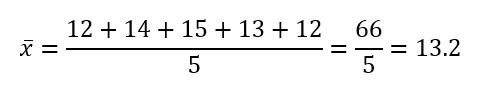
Mediana
La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenados de menor a mayor. Si el número de observaciones es impar, la mediana es el valor central. Si es par, la mediana es el promedio de los dos valores centrales.
Ejemplo:
Para las edades 12, 14, 15, 13, 12 (ordenadas: 12, 12, 13, 14, 15), la mediana es 13, ya que es el valor central.
Cálculo de la Mediana
- Ejemplo con 7 datos:
Datos: 5, 2, 8, 7, 3, 6, 4
Paso 1: Ordenar los datos de menor a mayor:
2, 3, 4, 5, 6, 7, 8
Paso 2: Identificar el valor central (el cuarto en este caso, ya que es un conjunto de 7 datos):
Mediana = 5
Cuando el número de datos es impar, la mediana es el valor que se encuentra en el centro del conjunto ordenado.
- Ejemplo con 8 datos:
Datos: 12, 7, 10, 9, 15, 11, 8, 14
Paso 1: Ordenar los datos de menor a mayor:
7, 8, 9, 10, 11, 12, 14, 15
Paso 2: Identificar los dos valores centrales (el cuarto y el quinto en este caso, ya que es un conjunto de 8 datos):
10 y 11
Paso 3: Calcular la media de estos dos valores centrales:
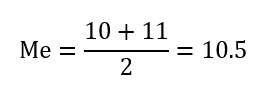
Cuando el número de datos es par, la mediana es el promedio de los dos valores centrales del conjunto ordenado.
Moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Un conjunto de datos puede tener una moda (unimodal), dos modas (bimodal), o más (multimodal). También puede no tener moda si todos los valores son únicos.
Ejemplo: En el conjunto de edades 12, 14, 15, 13, 12, la moda es 12, ya que aparece más veces que cualquier otro valor.
Ejemplo completo:
Consideremos el siguiente conjunto de datos de las notas de un examen de matemáticas: 7, 8, 7, 6, 9, 10, 6, 8, 7.
- Media:
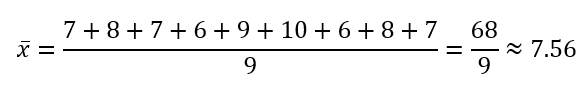
- Mediana:
Ordenando los datos: 6, 6, 7, 7, 7, 8, 8, 9, 10. La mediana es 7, ya que es el valor central del conjunto ordenado.
- Moda:
La moda es 7, ya que es el valor que más se repite en el conjunto de datos.
Aplicaciones

Control de Gastos Personales:
- Con gráficas de barras o histogramas, puedes visualizar la distribución de tus gastos mensuales por categorías (alimentación, transporte, entretenimiento, etc.). Esto te ayuda a identificar en qué áreas estás gastando más y ajustar tu presupuesto de manera efectiva.
Seguimiento de Actividad Física:
- Las aplicaciones de actividad física y salud suelen utilizar gráficos de barras y pictogramas para mostrar la cantidad de pasos diarios, calorías quemadas o minutos activos en la semana. Esto permite ver el progreso y ajustar rutinas según los objetivos de actividad.
Distribución de Tiempos de Tráfico:
- Los histogramas se utilizan para analizar el tiempo promedio de tráfico en ciertos horarios. Por ejemplo, en una ciudad, puedes ver en qué momentos del día el tráfico es más intenso y planificar tus trayectos para evitar los picos de congestión.
Encuestas de Satisfacción del Cliente:
- Los gráficos de barras son útiles para presentar los resultados de encuestas, como la satisfacción de clientes en una tienda. Esto facilita visualizar la opinión general sobre diferentes aspectos del servicio y ayuda a realizar mejoras específicas.
Monitoreo del Rendimiento Académico:
- Los profesores pueden usar gráficas de barras o pictogramas para mostrar el rendimiento de los estudiantes en diferentes áreas (exámenes, tareas, participación). Esto ayuda tanto a los docentes como a los estudiantes a identificar fortalezas y áreas de mejora en el aprendizaje.
