Acciones previas
Para sumar o restar los vectores de forma analítica, estos deben estar expresados primero en coordenadas rectangulares o vectores base.
De coordenadas polares a coordenadas rectangulares:
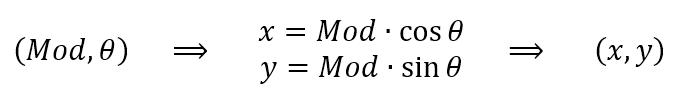
De coordenadas geográficas a coordenadas rectangulares:

Suma de vectores
Una vez expresados todos los vectores en coordenadas rectangulares, procedemos a sumar entre componentes correspondientes; es decir, sumamos entre las componentes “x” para obtener la componente “x” resultante, y sumamos entre las componentes “y” para obtener la componente “y” resultante.
Si tenemos los siguientes vectores:
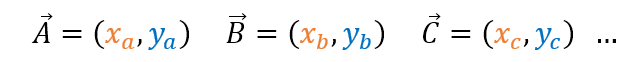
La suma de ellos sería:
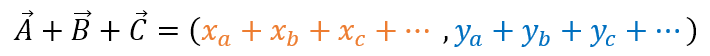
Suma de vectores gráficamente:
Para la suma de vectores de forma gráfica no es necesaria la transformación a coordenadas rectangulares.
Existen 2 métodos gráficos para la suma de vectores:
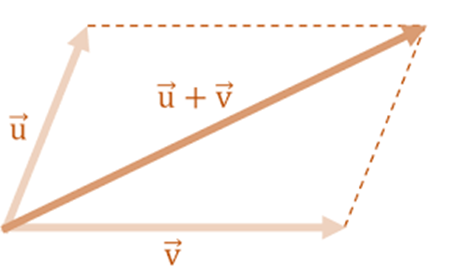
- Método del paralelogramo: Este método gráfico permite sumar 2 vectores a la vez. Si queremos sumas muchos vectores, debemos sumar de dos en dos: escogemos 2 vectores y los sumamos gráficamente con este método. Luego, el vector resultante lo sumamos con el siguiente vector, obteniendo un nuevo vector resultante. Y así sucesivamente.
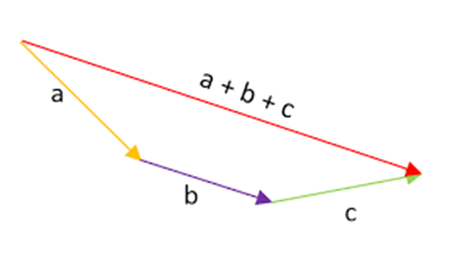
- Método del polígono: Este método gráfico permite sumar múltiples vectores a la vez, siguiendo este mecanismo: graficamos cualquiera de los vectores; colocamos el siguiente a partir del vector anterior; es decir, el origen del segundo vector colocamos en el extremo o “punta” del vector anterior. Es casi como colocar los vectores uno tras otro, como si se tratase a cada vector como los vagones de un tren.
Resta de vectores
La resta de vectores es en realidad una suma de vectores, solo que aquel vector antecedido por el signo negativo, se expresa como un nuevo vector con las mismas coordenadas pero con los signos contrarios, y se procede a sumar como lo indicado en la suma de vectores.
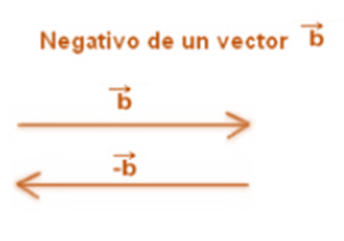
Gráficamente, un vector negativo se ve exactamente como el vector original, pero en sentido contrario. Es decir, si el vector b va hacia arriba, el vector -b va hacia abajo. Si el vector c va en cierto sentido, el vector c va en la misma dirección pero sentido contrario.
Si tenemos los siguientes vectores:
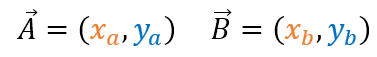
La suma de ellos sería:
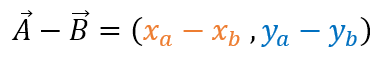
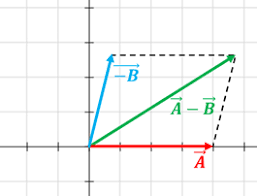
Resta de vectores gráficamente:
Los vectores antecedidos con signo negativo se representan gráficamente como un vector exactamente con la misma magnitud y dirección del vector original, pero en sentido contrario.
- Método del polígono: En este método, el vector resultante es uno que una “punta” con “punta” los vectores que están operando la resta. El sentido del vector depende del orden de la operación. Por ejemplo, si la resta es A-B, entonces la punta del vector resultante va en la punta de A, y el origen del vector resultante va en la punta de B. En ese orden.
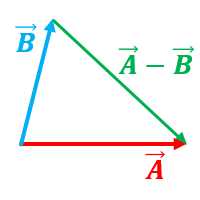
- Método del paralelogramo: Es igual que en la suma de vectores. Solo que uno de ellos se suma con el vector negativo del otro. Es decir, si los dos vectores son A y B, y se desea operar A-B, entonces el vector A se suma con -B (vector negativo de B).