Imagina que tienes varias cajas, y dentro de cada caja hay diferentes cantidades de frutas. Cada tipo de fruta está en una caja diferente: manzanas en una caja, plátanos en otra, naranjas en otra, y así sucesivamente.

Un polinomio es como una lista que te dice cuántas frutas tienes en cada caja. Pero en lugar de frutas, en matemáticas usamos números y letras (como x).
Learning goals:
- Definir qué es un polinomio y reconocer sus partes.
- Identificar y clasificar polinomios según su grado, términos y otras características.
- Aplicar el conocimiento de polinomios en situaciones del mundo real.
- Resolver problemas matemáticos que involucran polinomios de manera efectiva.
- Comparar diferentes tipos de polinomios y sus usos en diversas aplicaciones.
Revisemos primero…
¿Qué es un monomio?
Un monomio (también llamado “término”) es una expresión de un solo término. Pero… ¿Cómo lo identifico?¿Cómo lo distingo de otro?
Lo identificamos a través de sus partes, y los distinguimos de otros a través de sumas y restas. Vamos a ver un monomio como una “caja” de frutas.
Partes de un monomio
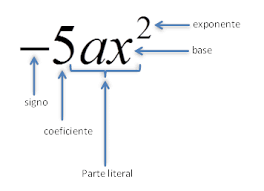
Coeficiente: Es el número que está multiplicando a la variable. Por ejemplo, en 3x, el 3 es el coeficiente.
Variable (en la parte literal): Es la letra que representa un número desconocido, normalmente representado por letras. En 3x, la variable (o parte literal) es x.
Exponente: Es el pequeño numerito que se encuentra justo encima de la variable, como si fuera su oreja derecha. Por ejemplo, en 4x2, el exponente es 2.
Signo: más ( + ) o menos ( – ). Se coloca al principio (lado izquierdo del resto del monomio).
Ejemplos de Monomios:
- 5x: Aquí, el coeficiente es 5, la variable es x, y el exponente (que no se ve) es 1.
- −3y2: Aquí, el coeficiente es −3, la variable es y, y el exponente es 2.
- 7: Este es un monomio que solo tiene un número (un coeficiente), sin variable. A veces se llama constante.
¿Qué hace a un monomio diferente de otros términos?
Un monomio solo tiene una parte (o “término”). No hay sumas o restas dentro de un monomio. Por ejemplo, 2x+3 no es un monomio porque tiene dos términos. Pero 2x es un monomio porque solo tiene un término, 3 es otro monomio porque también es solo un término. Es decir, que un monomio (término) se distingue de otro porque los separan símbolos de suma y resta (signos + y -). Cuando tenemos 2 o más monomios o “términos”, hablamos de polinomios.
¡Identifiquemos a los polinomios!
Dicho de forma simple, un polinomio está compuesto de 1, 2 o más monomios o “términos”, separados por símbolos de suma y resta (signos + y -).
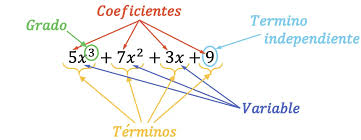
Partes de un polinomio
- Términos: ¿Recuerdas que al principio hablábamos de las “cajas” con frutas? Cada una de las “cajas” en un polinomio se llama un término. Un término es una combinación de un número (llamado coeficiente) y una letra (llamada variable), tal y como se explicó más arriba. Por ejemplo, 3x2 es un término donde 3 es el coeficiente y x2 es la variable.
- Suma de términos: Un polinomio es simplemente una suma de varios términos. Por ejemplo, 4x2+3x+5 es un polinomio con tres términos: 4x2, 3x, y 5.
- Grado del polinomio: El grado de un polinomio es como la caja más grande, o el término con la letra elevada al número más alto. Por ejemplo, en 4x2+3x+5, el grado del polinomio es 2, porque el término 4x2 tiene la x elevada al cuadrado.

Clasificación de los polinomios
Está claro que, cuando tenemos 1 o más términos, la expresión es un polinomio. Los polinomios compuestos por solo 1 término, se llaman monomios; lo que tienen 2 términos; se llaman binomios, los que tienen 3 términos, trinomios; y los que tienen más, simplemente los seguiremos llamando polinomios.
Ejemplos de binomios:

Ejemplos de trinomios:
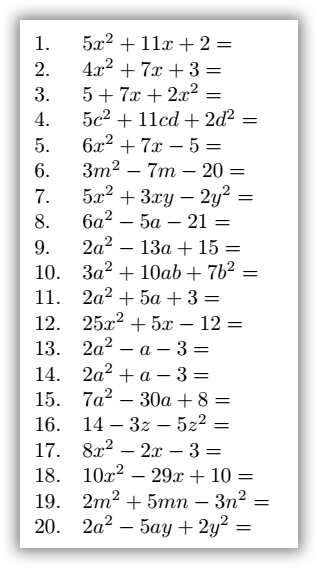
Ejemplos de polinomios:


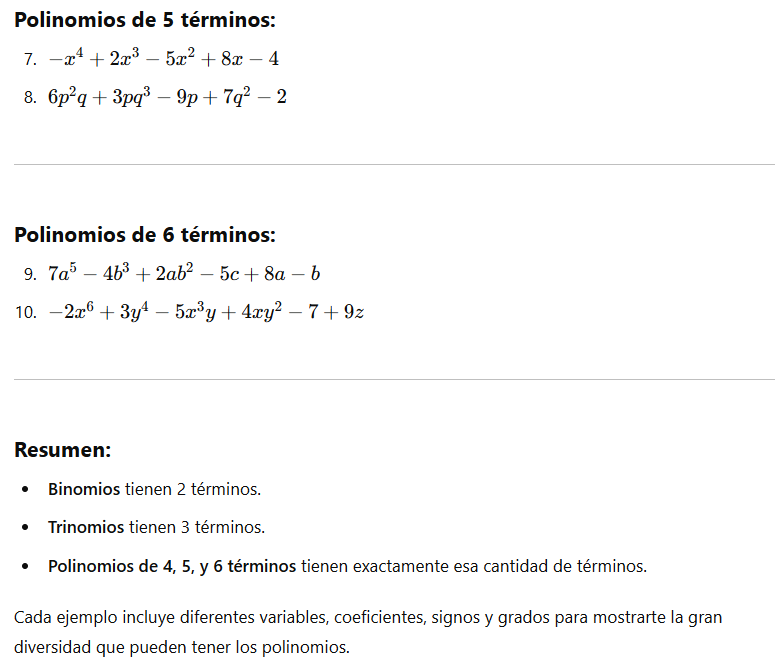
Términos semejantes

Resources:
Learning activities:
Adaptaciones curriculares:
–
–
–
–
