División de polinomios

¿Alguna vez te has preguntado cómo los matemáticos dividen polinomios de una forma más ágil? ¡Hoy vas a descubrir el mágico método de Ruffini! Este método te permitirá realizar divisiones de polinomios de manera rápida y eficiente. Además, exploraremos el Teorema del Resto, que te ayudará a entender el comportamiento de los polinomios cuando se dividen por binomios de la forma 𝑥 − 𝑎

---

Learning goals:

• Comprender el método de división de polinomios a través de Ruffini.
• Aplicar el método de Ruffini para dividir polinomios.
• Entender el Teorema del Resto y su aplicación en polinomios.
• Resolver problemas de división de polinomios utilizando el método de Ruffini.
• Aplicar el Teorema del Resto en diversos problemas matemáticos.

---

Método de Ruffini

Paso 1: Escribir el polinomio y el divisor

• Considera el polinomio 𝑃(𝑥) y el binomio divisor de la forma 𝑥−𝑎.
• Asegúrate de que el polinomio esté ordenado según las potencias decrecientes de 𝑥.

Paso 2: Coeficientes del polinomio

Extrae los coeficientes del polinomio 𝑃(𝑥).

Paso 3: Aplicar Ruffini

• Coloca 𝑎 (el término del binomio 𝑥−𝑎) a la izquierda de una línea vertical y los coeficientes del polinomio a la derecha.
• Baja el primer coeficiente.
• Multiplica este coeficiente por 𝑎 y coloca el resultado debajo del segundo coeficiente.
• Suma esta columna y repite el proceso para cada coeficiente.

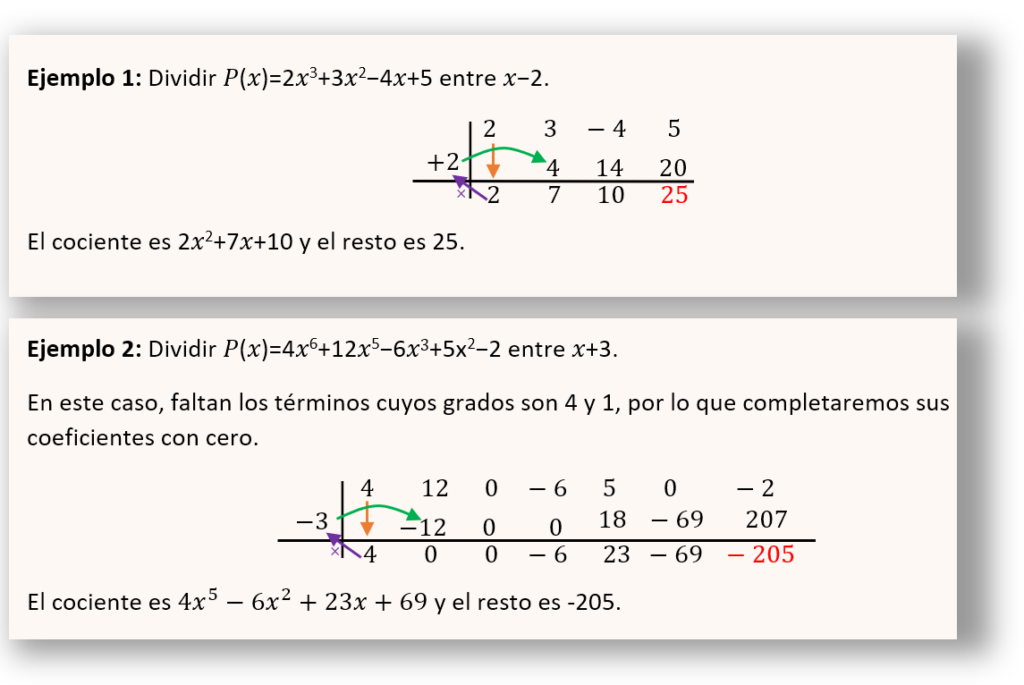
Teorema del Resto

El Teorema del Resto afirma que, al dividir un polinomio P(x) por un binomio de la forma x−a, el resto de la división es P(a).

Paso a paso:

1. Escribe el polinomio P(x).
2. Sustituye x por a.
3. Calcula P(a).

---

Ejercicios propuestos:

Grupo de ejercicios 1

Grupo de ejercicios 2

Grupo de ejercicios 3

Resources:

---

---

Learning activities:

Adaptaciones curriculares:
–
–
–
–