
¡Bienvenidos a una aventura matemática! Hoy nos sumergiremos en el fascinante mundo de las ecuaciones e inecuaciones de una variable. Imagínate que estamos armando un rompecabezas, donde cada pieza es un número o una letra que debemos colocar en el lugar correcto para resolver el misterio. ¿Te gustaría dominar la técnica para resolver ecuaciones desde las más sencillas hasta las más complejas usando el método de Ruffini? ¡Acompáñame en este viaje y descubre que las matemáticas pueden ser tan emocionantes como resolver un enigma!
Learning goals:
- Entender el concepto de ecuaciones e inecuaciones de una variable.
- Identificar y resolver ecuaciones de primer a quinto grado factorizables en factores binomiales de primer grado.
- Aplicar el método de Ruffini para resolver ecuaciones e inecuaciones.
- Desarrollar habilidades de factorización y simplificación de ecuaciones.
- Resolver ejercicios prácticos para consolidar el aprendizaje.
Ecuaciones de una Variable
Ecuaciones de Primer Grado
Una ecuación de primer grado tiene la forma ax+b=0. La solución de esta ecuación es sencilla:
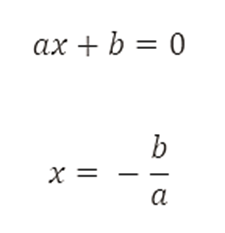

Ecuaciones de Segundo Grado
Una ecuación de segundo grado tiene la forma ax2+bx+c=0. Si es factorizable, podemos resolverla usando factores binomiales de primer grado.
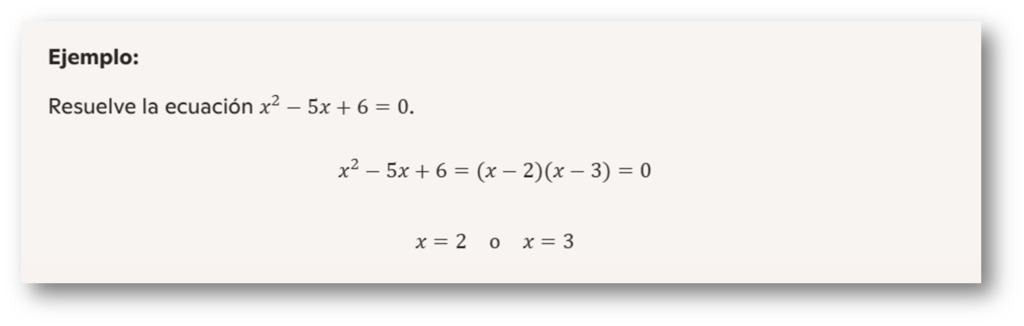
Ecuaciones de Tercer Grado
Para una ecuación de tercer grado factorizable, podemos usar el método de Ruffini.

Ecuaciones de Grados Superiores
Para ecuaciones de grados superiores, el proceso es similar, pero con más pasos de factorización y uso del método de Ruffini.
Para factorizar a través de Ruffini, puedes ver los videos que se encuentran en la sección Resources de esta lección.
Para resolver en clase:


Inecuaciones de una Variable
Recordemos algunas cosas:
Elementos de la inecuación
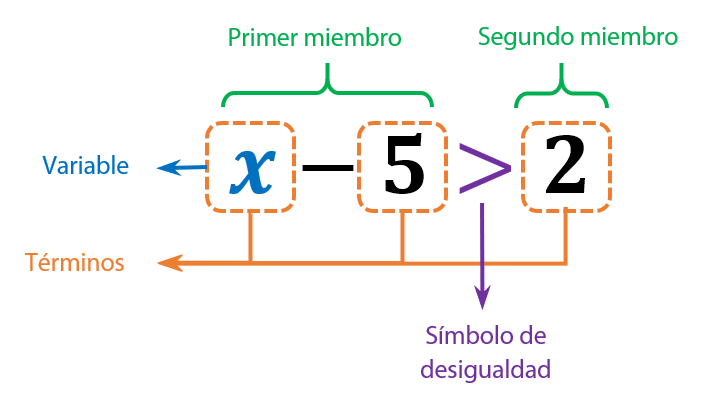
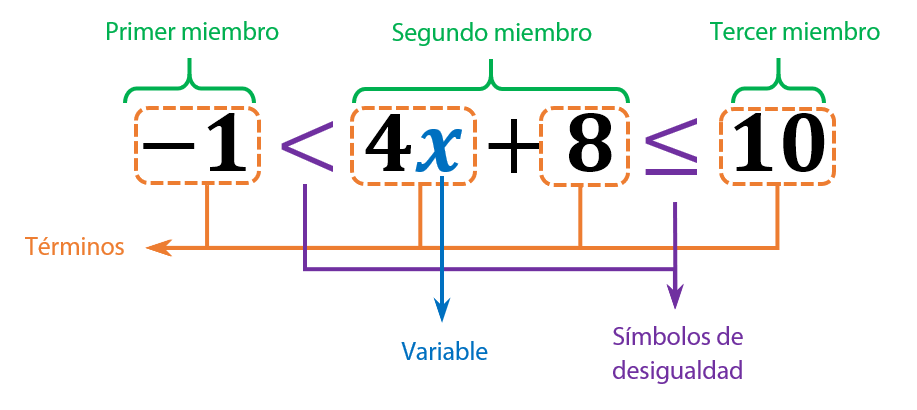
Miembros: En una inecuación, los miembros son las dos expresiones que se encuentran a cada lado del símbolo de la inecuación. Por ejemplo, en la inecuación 2x+3>5, los miembros son, el de la izquierda (primer miembro) 2x+3, y el de la derecha (segundo miembro) 5.
Términos: Los términos son los elementos individuales que componen los miembros de la inecuación, separados los los símbolos de suma (+) y resta (-). Estos pueden ser números, variables o productos de números y variables. En la inecuación 2x+3>5, los términos son 2x y 3 en el primer miembro, y 5 en el segundo miembro.
Variable: La variable es el símbolo que representa un valor desconocido que queremos determinar. En las inecuaciones, las variables suelen ser letras como x, y, z, etc. En la inecuación 2x+3>5, la variable es x.
Símbolo de la inecuación: El símbolo de la inecuación es el signo que indica la relación de desigualdad entre los dos miembros de la inecuación. Los símbolos más comunes son:
- >: mayor que
- ≥: mayor o igual que
- <: menor que
- ≤: menor o igual que
Por ejemplo, en la inecuación 2x+3>5, el símbolo > indica que el primer miembro es mayor que el segundo miembro.
Intervalos
La solución de una inecuación se presenta como un intervalo, y no como solución única. Lo explicaremos mejor: una solución única es aquella que determina un único valor para una incógnita. Por ejemplo, x=2 indica que “x” vale 2 y no otro valor, tal y como sucedió en el tema de ecuaciones. Por otro lado, en las inecuaciones, un intervalo es un rango de valores que puede tomar una incógnita (a la que llamaremos variable porque puede variar en su valor) desde un “inicio” hasta un “fin”, de tal manera que los valores en ese rango cumplan con lo indicado con la inecuación. Por ejemplo, [3, 5] indica que “x” puede tomar cualquier valor desde el 3 hasta el 5, incluyendo números decimales. No te preocupes por la notación que acabas de leer. Lo explicaremos a continuación.
Notación de intervalos
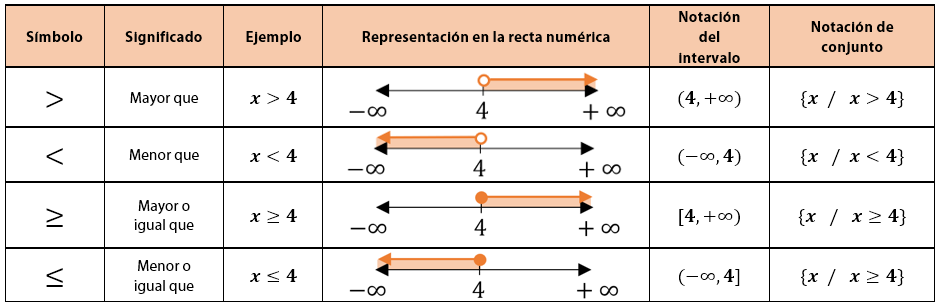
Antes de pasar a la representación de intervalos en la variedad de sus notaciones, te explicaremos qué significan los símbolos utilizados, en la tabla a continuación:

Nota: los infinitos siempre son abiertos.
Por ejemplo:
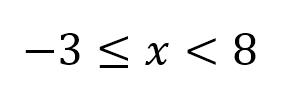
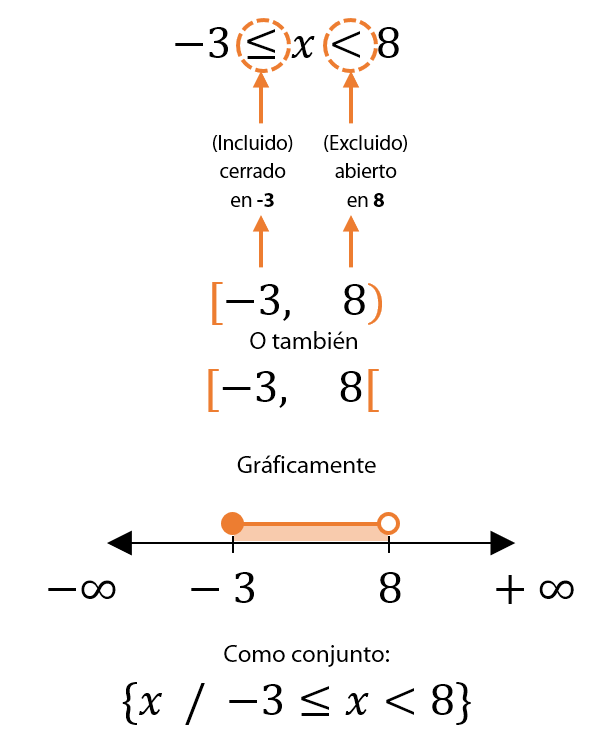
En el ejemplo, la solución de “x” está entre los valores que van desde -3 hasta 8, pero con las siguientes consideraciones:
- -3 está incluido en la solución, puesto que el símbolo que lo acompaña es ≤, le corresponde un corchete cerrado, “comiendo” al número -3, y en representación gráfica le corresponde un punto pintado ●.
- 8 está excluido de la solución, puesto que el símbolo que lo acompaña es <, le corresponde un corchete abierto, “dándole la espalda” al número 8, y en representación gráfica le corresponde un punto despintado ◯.
Otros ejemplos:
Inecuaciones de Primer Grado
Las inecuaciones siguen un proceso similar a las ecuaciones, pero con desigualdades. Las ecuaciones vistas en el apartado anterior son un ejemplo de inecuaciones de primer grado.

Inecuaciones de Grado Superior
Podemos aplicar factorización y el método de Ruffini para encontrar las soluciones.
Aplicamos una tabla de evaluación para hallar los intervalos solución de la inecuación de grado superior a 1.


Con esto, la inecuación original quedaría así:
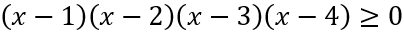
Cada factor igualamos a cero y obtenemos las raíces, que serán los límites de los intervalos que evaluaremos para hallar la solución:
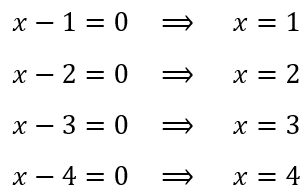
Los evaluamos en una tabla: En los divisores de las columnas colocaremos en los extremos, los infinitos, y en los divisores medios, las raíces en el orden de la recta numérica. En las filas, colocaremos cada uno de los factores que vamos a evaluar. Además, como el símbolo de la inecuación es mayor o igual que cero (), escogeremos los intervalos positivos (+) de la ley de signos de cada columna. Los puntos son pintados debido al símbolo de la inecuación.
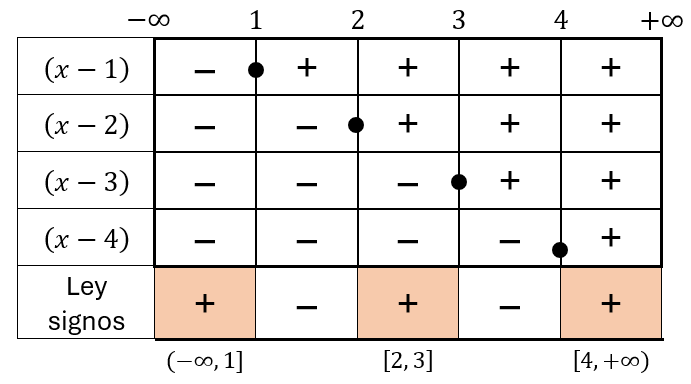
La solución es:
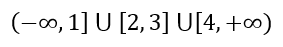
Es decir, que cualquier valor que sea menor a 1, o esté entre 2 y 3, o sea mayor que 4, incluidos los valores 1, 2, 3, y 4, al reemplazarlo en la inecuación cumplirá con la condición de esta.
Resources:
Learning activities:
Resuelve las siguientes ecuaciones

Resuelve las siguientes inecuaciones

Adaptaciones curriculares:
–
–
–
–
