
La estadística es una disciplina fundamental que nos ayuda a entender y tomar decisiones informadas a partir de datos. A través del análisis estadístico, podemos identificar patrones, hacer predicciones y comprender la variabilidad en los datos. En esta lección, haremos un repaso de los conceptos básicos de estadística, proporcionando una base sólida para aquellos que buscan refrescar sus conocimientos o aprender desde cero.
Learning goals:
- Diferenciar entre variables cuantitativas (discretas y continuas) y cualitativas (nominales y ordinales).
- Comprender la diferencia entre población y muestra.
- Calcular y entender las medidas de tendencia central: media, mediana y moda.
- Calcular y comprender las medidas de dispersión: rango, desviación media, varianza y desviación estándar.
- Interpretar y construir diferentes tipos de gráficas estadísticas: barras, histogramas, diagramas de caja y bigotes, pastel, radiales y de puntos.
Repaso de conceptos básicos
- Variables (Datos)
- Cuantitativas:
- Discretas: Son aquellas que pueden tomar un número finito de valores. Ejemplo: número de estudiantes en una clase.
- Continuas: Pueden tomar cualquier valor dentro de un intervalo. Ejemplo: peso de una persona.
- Cualitativas:
- Nominales: No tienen un orden específico. Ejemplo: colores de ojos (azul, verde, marrón).
- Ordinales: Tienen un orden natural. Ejemplo: clasificación de satisfacción (insatisfecho, neutral, satisfecho).
- Cuantitativas:
- Población y muestra
- Población: Conjunto completo de todos los elementos que se desean estudiar. Ejemplo: todos los estudiantes de una universidad.
- Muestra: Subconjunto representativo de la población. Ejemplo: 200 estudiantes seleccionados al azar de una universidad.
- Medidas de tendencia central
- Media:
- Suma de todos los valores dividida por el número de valores. Ejemplo: (5 + 10 + 15) / 3 = 10.
- Mediana:
- Para un número impar de elementos: Valor central. Ejemplo: {3, 5, 7} → Mediana = 5.
- Para un número par de elementos: Promedio de los dos valores centrales. Ejemplo: {2, 4, 6, 8} → Mediana = (4 + 6) / 2 = 5.
- Moda:
- Valor que más se repite.
- Monomodal: {1, 2, 2, 3} → Moda = 2.
- Multimodal: {1, 2, 2, 3, 3} → Modas = 2 y 3.
- Sin moda: {1, 2, 3, 4} → No hay moda.
- Media:
- Medidas de dispersión
- Rango: Diferencia entre el valor máximo y mínimo. Ejemplo: {2, 4, 7, 10} → Rango = 10 – 2 = 8.
- Desviación media: Promedio de las diferencias absolutas respecto a la media.
- Varianza: Promedio de las diferencias al cuadrado respecto a la media.
- Desviación estándar: Raíz cuadrada de la varianza.
- Medidas de posición
- Cuantiles: Dividen los datos en partes iguales.
- Cuartiles: Dividen los datos en cuatro partes. Ejemplo: Q1, Q2 (mediana), Q3.
- Deciles: Dividen los datos en diez partes.
- Percentiles: Dividen los datos en cien partes.
- Tipos de gráficas
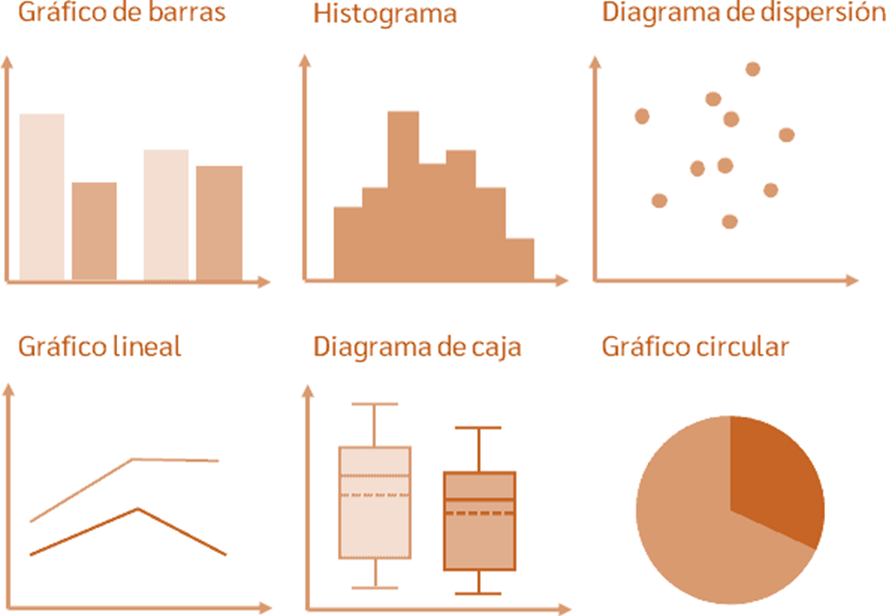
- Gráficas de barras: Representan datos categóricos con barras de diferentes alturas.
- Histogramas: Representan la distribución de datos cuantitativos.
- Diagramas de caja y bigotes: Muestran la distribución de datos a través de sus cuartiles.
- Gráficas de pastel: Representan datos categóricos en forma de un círculo dividido en sectores.
- Gráficas radiales: También conocidas como gráficas de araña, representan datos multivariables.
- Gráficas de puntos: Representan datos individuales como puntos en un gráfico.
Resources:
Learning activities:
Adaptaciones curriculares:
–
–
–
–
