
En el vasto mundo de las matemáticas, las funciones reales son fundamentales para describir y entender diversas relaciones y comportamientos en la naturaleza, la economía, y más allá. Estudiar las funciones reales no solo nos proporciona herramientas poderosas para resolver problemas prácticos, sino que también nos permite ver la belleza y la lógica en patrones que quizás pasen desapercibidos en la vida diaria. ¡Emprendamos este viaje para explorar y dominar el concepto de funciones reales!
Learning goals:
- Definir el concepto y estructura de una función real.
- Identificar y calcular el dominio y el rango de una función.
- Determinar el grado de una función y comprender su importancia.
- Encontrar las raíces, ceros o soluciones de una función y sus intersecciones con los ejes.
- Analizar la monotonía y la simetría de una función, y comprender cómo se identifican los máximos y mínimos absolutos y relativos.
Concepto y Estructura de una Función
Una función real es una relación que asigna a cada valor del conjunto de entrada (dominio) un único valor en el conjunto de salida (codominio). La regla de correspondencia define cómo se realiza esta asignación.
Ejemplo:
f(x)=x2+2x−3f(x) = x^2 + 2x – 3
Dominio y Rango
- Dominio: Conjunto de todos los valores posibles de la variable independiente xx para los cuales la función está definida.
- Rango: Conjunto de todos los valores posibles de la variable dependiente yy obtenidos al aplicar la función al dominio.
Ejemplos:
- Dominio: Para f(x)=x−1f(x) = \sqrt{x-1}, el dominio es [1,∞)[1, \infty).
- Rango: Para g(x)=x2g(x) = x^2, el rango es [0,∞)[0, \infty).
Grado de una Función
El grado de una función polinómica es el mayor exponente de la variable xx en su expresión algebraica. El grado de una función determina la forma general de su gráfica y el comportamiento de la función en valores extremos de xx.
Ejemplo:
Para f(x)=3×4−2×3+x−5f(x) = 3x^4 – 2x^3 + x – 5, el grado es 4.
Raíces, Ceros o Soluciones
Las raíces o ceros de una función son los valores de xx para los cuales f(x)=0f(x) = 0. Estos puntos representan las intersecciones de la gráfica de la función con el eje xx.
Ejemplo:
Para f(x)=x2−4f(x) = x^2 – 4, las raíces son x=2x = 2 y x=−2x = -2.
Cortes o Intersecciones con los Ejes
- Intersección con el eje xx: Los puntos donde y=0y = 0 (raíces de la función).
- Intersección con el eje yy: El punto donde x=0x = 0.
Ejemplo:
Para f(x)=x2−4x+4f(x) = x^2 – 4x + 4, la intersección con el eje yy es (0,4)(0, 4).
Máximos y Mínimos Absolutos y Relativos
- Máximos y mínimos absolutos: Los valores más altos y más bajos que la función alcanza en todo su dominio.
- Máximos y mínimos relativos: Los valores más altos y más bajos que la función alcanza en intervalos específicos de su dominio.
Ejemplo:
Para f(x)=−x2+4x−3f(x) = -x^2 + 4x – 3, el máximo relativo es en x=2x = 2 y y=1y = 1.
Monotonía
Una función es creciente si su valor aumenta a medida que xx aumenta, y es decreciente si su valor disminuye a medida que xx aumenta.
Ejemplo:
Para f(x)=x3−3×2+2f(x) = x^3 – 3x^2 + 2, es creciente en (−∞,1)∪(2,∞)(-\infty, 1) \cup (2, \infty) y decreciente en (1,2)(1, 2).
Simetría
- Simetría Par: Una función es par si f(−x)=f(x)f(-x) = f(x) para todos los xx en el dominio.
- Simetría Impar: Una función es impar si f(−x)=−f(x)f(-x) = -f(x) para todos los xx en el dominio.
Ejemplos:
- Función Par: f(x)=x2f(x) = x^2
- Función Impar: g(x)=x3g(x) = x^3
Tipos de Funciones
1. Polinómicas
Características: Funciones que se pueden expresar como f(x)=anxn+an−1xn−1+…+a1x+a0f(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0.
1.1. Función Constante
- Dominio: Todos los números reales (R\mathbb{R}).
- Recorrido: Un único valor constante.
- Cortes con los ejes: No tiene cortes con el eje xx, y corta el eje yy en el valor constante.
- Monotonía: No es creciente ni decreciente, es constante.
1.2. Función Lineal y Función Afín
- Dominio: Todos los números reales (R\mathbb{R}).
- Recorrido: Todos los números reales (R\mathbb{R}).
- Cortes con los ejes: Corta el eje yy en (0,b)(0, b) y el eje xx en x=−bmx = -\frac{b}{m}.
- Simetría: Generalmente ninguna, excepto si b=0b = 0.
- Monotonía: Creciente si m>0m > 0, decreciente si m<0m < 0.
1.3. Función Cuadrática
- Dominio: Todos los números reales (R\mathbb{R}).
- Recorrido: Depende de la concavidad.
- Cortes con los ejes: Puede cortar el eje xx en 0, 1 o 2 puntos y el eje yy en (0,c)(0, c).
- Monotonía: Depende de la concavidad (abierta hacia arriba o hacia abajo).
- Vértice: Punto de máximo o mínimo.
- Simetría: Siempre simétrica respecto al eje yy.
1.4. Función Cúbica
- Dominio: Todos los números reales (R\mathbb{R}).
- Recorrido: Todos los números reales (R\mathbb{R}).
- Cortes con los ejes: Hasta 3 raíces (cortes con el eje xx) y corta el eje yy en (0,d)(0, d).
- Monotonía: Intervalos crecientes y decrecientes.
- Máximos y Mínimos Relativos: Pueden tener uno o dos puntos de inflexión.
- Simetría: Generalmente impar (simétrica respecto al origen).
2. Funciones Racionales
Características: Funciones que se pueden expresar como el cociente de dos polinomios.
- Condiciones de Dominio y Rango: El dominio excluye los valores que hacen que el denominador sea cero.
- Asíntotas: Horizontales y verticales se determinan analizando el comportamiento en los límites y cuando el denominador es cero.
- Cortes con los ejes: Determinadas por los ceros del numerador y la evaluación de x=0x = 0 en la función.
- Monotonía: Determinada por la derivada primera.
- Máximos y Mínimos Relativos: Determinados por los puntos críticos y la derivada segunda.
- Simetría: Puede ser par, impar o ninguna.
3. Funciones Radicales
Características: Funciones que incluyen raíces (por ejemplo, raíces cuadradas).
- Condiciones de Dominio y Rango: El dominio depende de asegurar que la expresión bajo la raíz sea no negativa (para raíces pares).
- Asíntotas: Determinadas en límites.
- Cortes con los ejes: Determinados por los ceros y evaluaciones en el origen.
- Monotonía: Determinada por la derivada.
- Máximos y Mínimos Relativos: Determinados por los puntos críticos y análisis de la derivada.
- Simetría: Puede ser par, impar o ninguna, dependiendo de la función específica.
Resources:
Learning activities:
Ejercicios Propuestos
Ejercicio 1: Dominio y Rango
Determina el dominio y el rango de las siguientes funciones:
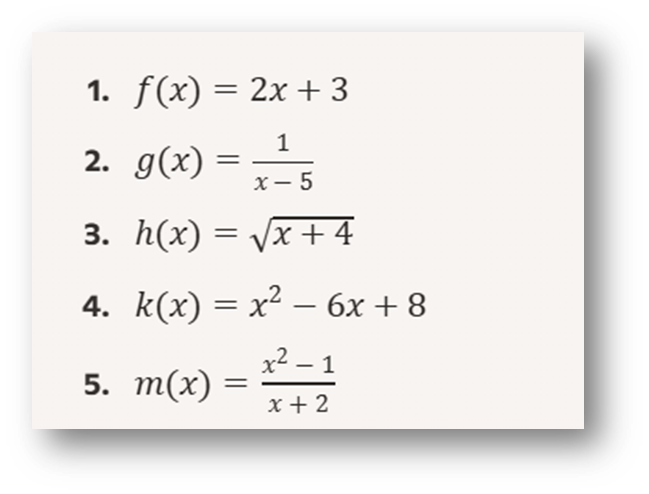
Ejercicio 2: Grado de la Función
Identifica el grado de las siguientes funciones polinómicas y describe el comportamiento general de su gráfica:
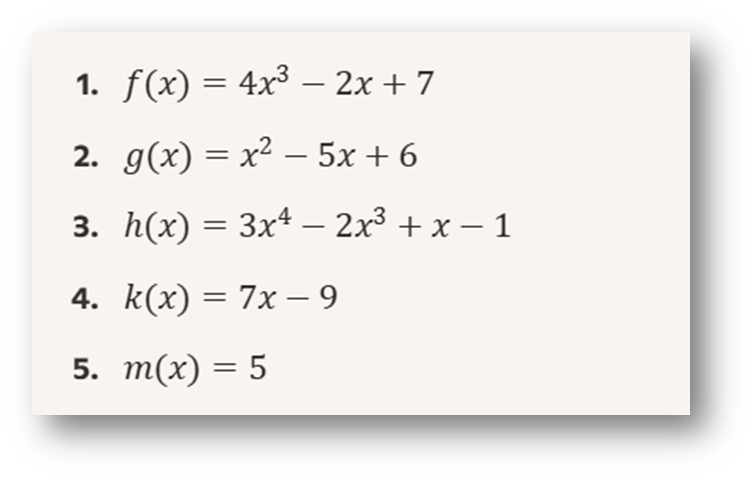
Ejercicio 3: Raíces, Ceros o Soluciones
Encuentra las raíces de las siguientes funciones:
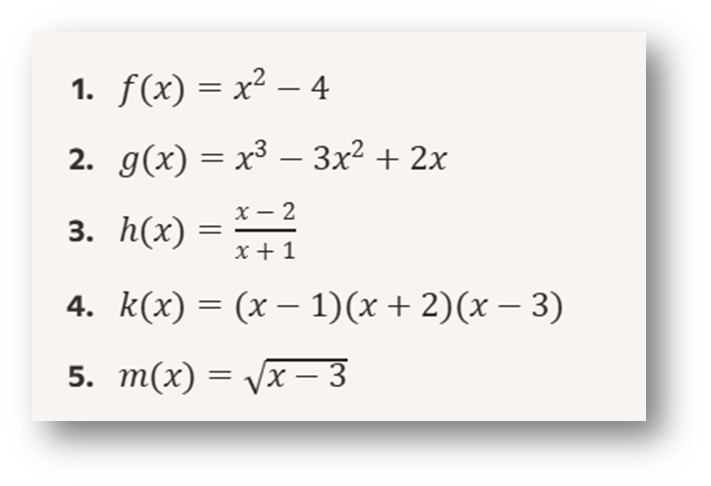
Ejercicio 4: Cortes con los Ejes
Determina los puntos de intersección con los ejes x y y de las siguientes funciones:
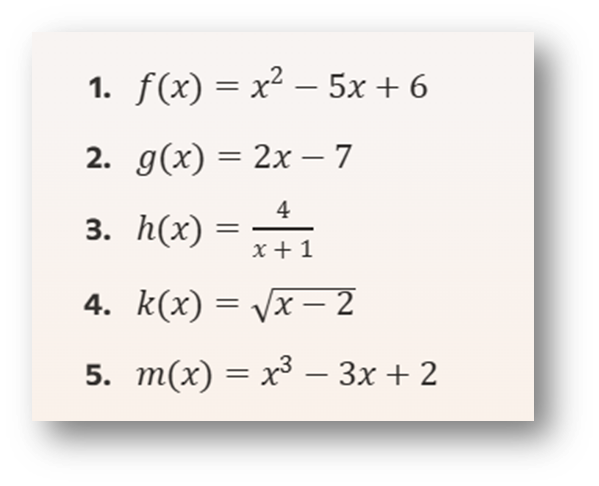
Ejercicio 5: Máximos y Mínimos Relativos y Absolutos
Encuentra los máximos y mínimos relativos y absolutos, si existen, de las siguientes funciones:
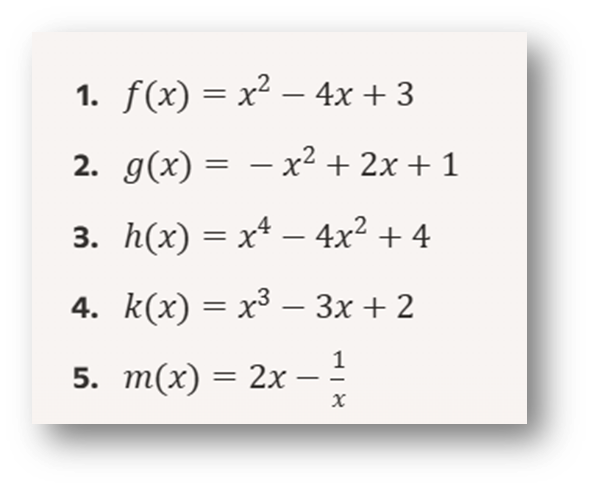
Ejercicio 6: Monotonía
Determina los intervalos donde las siguientes funciones son crecientes y decrecientes:
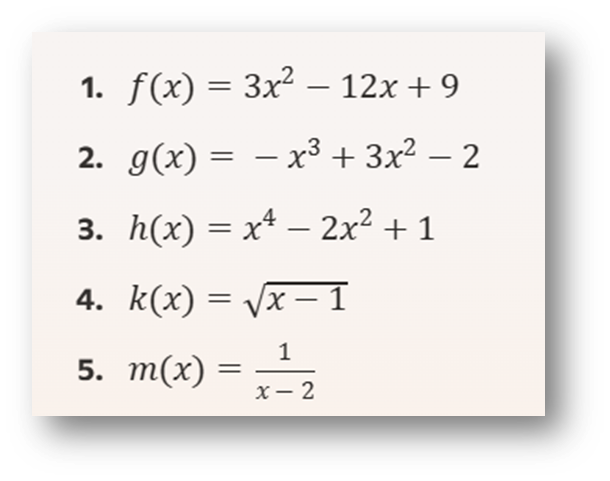
Ejercicio 7: Simetría
Determina si las siguientes funciones son pares, impares o ninguna:
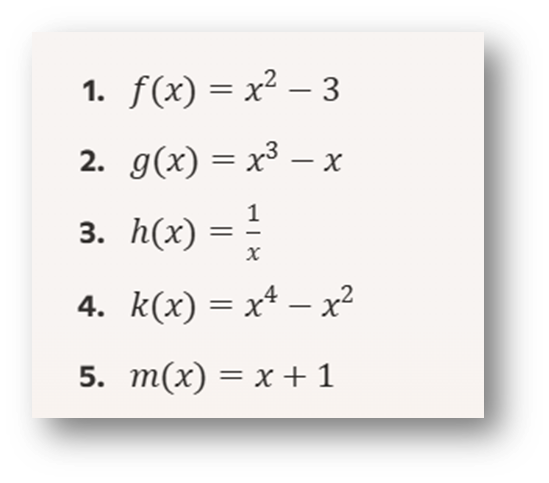
Ejercicio 8: Tipos de Funciones
Identifica el tipo de cada una de las siguientes funciones y proporciona su dominio, rango, cortes con los ejes y comportamiento de monotonía:
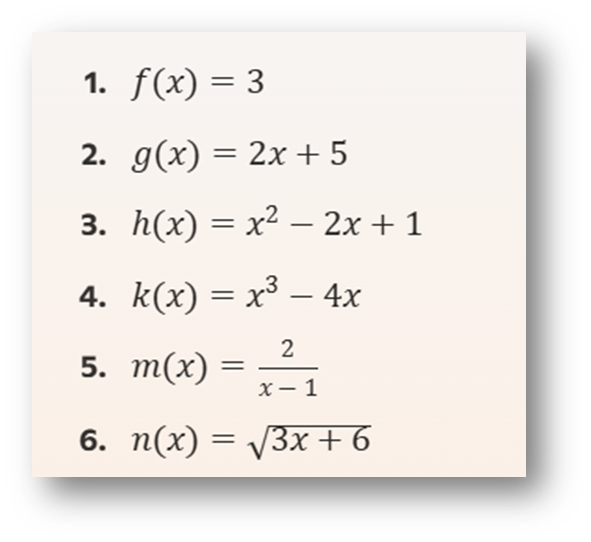
Ejercicio 9: Funciones Racionales
Para cada función racional, encuentra el dominio, las asíntotas, los cortes con los ejes y la monotonía:
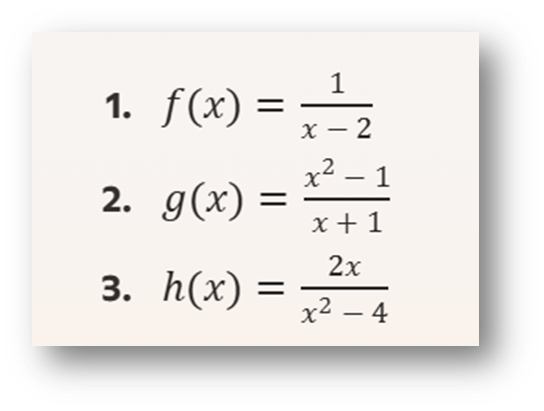
Ejercicio 10: Funciones Radicales
Para cada función radical, encuentra el dominio, las asíntotas, los cortes con los ejes y la monotonía:
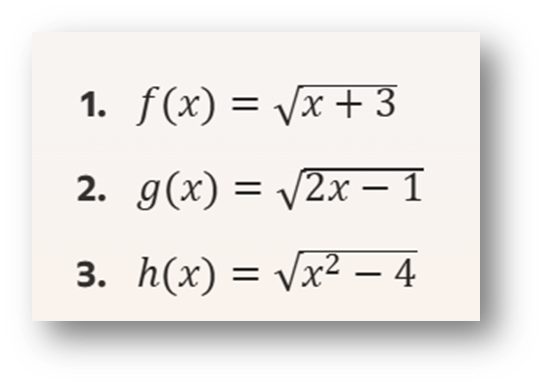
Adaptaciones curriculares:
Resuelve la cuarta parte de cada grupo de ejercicios.
