Traslación de funciones

Las traslaciones de funciones son una herramienta poderosa en el análisis de funciones y sus gráficas. Imagina poder mover toda una gráfica sin cambiar su forma, simplemente desplazándola hacia arriba, abajo, a la izquierda o a la derecha. Esta habilidad es crucial para resolver problemas complejos y modelar situaciones del mundo real de manera más efectiva. ¡Vamos a explorar juntos cómo las traslaciones de funciones pueden transformar nuestra comprensión de las matemáticas!

---

Learning goals:

Al finalizar esta lección, podrás:

1. Comprender el concepto de traslación de funciones y su importancia en el análisis matemático.
2. Identificar las diferentes formas de traslación de funciones.
3. Aplicar traslaciones verticales y horizontales a funciones.
4. Analizar el impacto de las traslaciones en las gráficas de funciones.
5. Resolver problemas prácticos utilizando traslaciones de funciones.

---

Pasos claros y detallados sobre cada aspecto en la traslación de funciones

1. Traslación Vertical

Una traslación vertical mueve la gráfica de una función hacia arriba o hacia abajo sin cambiar su forma.

Paso 1: Dada una función f(x)f(x), una traslación hacia arriba por kk unidades se representa como f(x)+kf(x) + k.

Paso 2: Una traslación hacia abajo por kk unidades se representa como f(x)−kf(x) – k.

Ejemplo:

Para la función f(x)=x2f(x) = x^2:

• Traslación hacia arriba por 3 unidades: f(x)=x2+3f(x) = x^2 + 3
• Traslación hacia abajo por 2 unidades: f(x)=x2−2f(x) = x^2 – 2

2. Traslación Horizontal

Una traslación horizontal mueve la gráfica de una función hacia la izquierda o hacia la derecha sin cambiar su forma.

Paso 1: Dada una función f(x)f(x), una traslación hacia la derecha por hh unidades se representa como f(x−h)f(x – h).

Paso 2: Una traslación hacia la izquierda por hh unidades se representa como f(x+h)f(x + h).

Ejemplo:

Para la función f(x)=x2f(x) = x^2:

• Traslación hacia la derecha por 4 unidades: f(x)=(x−4)2f(x) = (x – 4)^2
• Traslación hacia la izquierda por 3 unidades: f(x)=(x+3)2f(x) = (x + 3)^2

3. Combinación de Traslaciones

Las traslaciones combinadas permiten mover la gráfica en ambas direcciones, vertical y horizontalmente, simultáneamente.

Paso 1: Identifica la función base f(x)f(x).

Paso 2: Aplica la traslación horizontal: f(x−h)f(x – h) o f(x+h)f(x + h).

Paso 3: Aplica la traslación vertical al resultado del paso 2: f(x−h)+kf(x – h) + k o f(x+h)+kf(x + h) + k.

Ejemplo:

Para la función f(x)=x2f(x) = x^2:

• Traslación hacia la derecha por 2 unidades y hacia arriba por 3 unidades: f(x)=(x−2)2+3f(x) = (x – 2)^2 + 3
• Traslación hacia la izquierda por 1 unidad y hacia abajo por 4 unidades: f(x)=(x+1)2−4f(x) = (x + 1)^2 – 4

Ejemplos

Ejemplo 1: Traslación Vertical

• Dada la función f(x)=xf(x) = \sqrt{x}, una traslación hacia arriba por 5 unidades es f(x)=x+5f(x) = \sqrt{x} + 5.

Ejemplo 2: Traslación Horizontal

• Dada la función f(x)=xf(x) = \sqrt{x}, una traslación hacia la izquierda por 3 unidades es f(x)=x+3f(x) = \sqrt{x + 3}.

Ejemplo 3: Combinación de Traslaciones

• Dada la función f(x)=xf(x) = \sqrt{x}, una traslación hacia la derecha por 2 unidades y hacia abajo por 4 unidades es f(x)=x−2−4f(x) = \sqrt{x – 2} – 4.

Resources:

---

Learning activities:

Ejercicios Propuestos

Ejercicio 1: Traslación Vertical

Realiza las siguientes traslaciones verticales y grafica las funciones originales y trasladas:

Ejercicio 2: Traslación Horizontal

Realiza las siguientes traslaciones horizontales y grafica las funciones originales y trasladas:

Ejercicio 3: Combinación de Traslaciones

Realiza las siguientes combinaciones de traslaciones y grafica las funciones originales y trasladas:

Ejercicio 4: Identificación de Traslaciones

Identifica las traslaciones realizadas en las siguientes funciones y describe los movimientos:

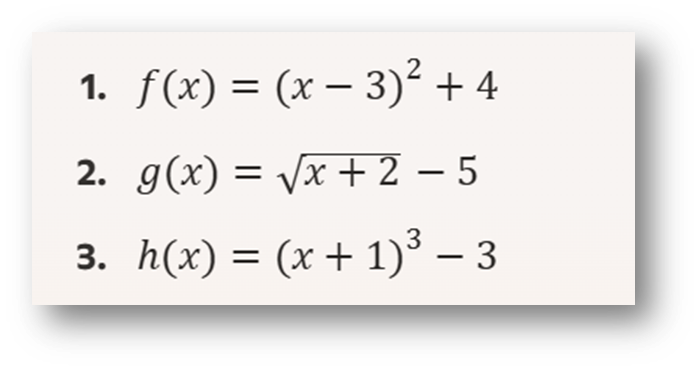
Ejercicio 5: Aplicación Práctica

Resuelve los siguientes problemas prácticos utilizando traslaciones de funciones:

Adaptaciones curriculares:

Resuelve la mitad de cada grupo de ejercicios.