Concepto de Logaritmo

¿Alguna vez te has preguntado cómo los científicos y matemáticos manejan números increíblemente grandes o pequeños sin volverse locos? Aquí es donde los logaritmos entran en juego. Los logaritmos son una herramienta matemática poderosa que nos permite simplificar cálculos complicados, resolver ecuaciones exponenciales, y explorar la relación entre números en formas fascinantes. En esta lección, desentrañaremos el misterioso mundo de los logaritmos y descubriremos cómo se aplican en la vida diaria.

---

Learning goals:

Al final de esta lección, tú serás capaz de:

1. Comprender el concepto básico de un logaritmo y su relación con las potencias.
2. Resolver ecuaciones logarítmicas y exponenciales con confianza.
3. Aplicar propiedades de los logaritmos para simplificar expresiones complejas.
4. Interpretar y usar logaritmos en contextos científicos y financieros.
5. Reconocer y utilizar logaritmos en situaciones de la vida diaria.

---

Conceptos básicos

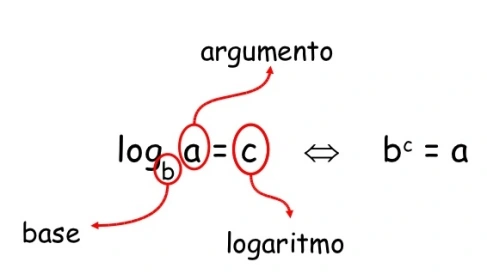
Un logaritmo es una manera de expresar exponentes. Por ejemplo, si b^c=a, entonces log⁡_ba=c. Este concepto se vuelve útil cuando necesitamos trabajar con números muy grandes o muy pequeños.

Partes de un Logaritmo

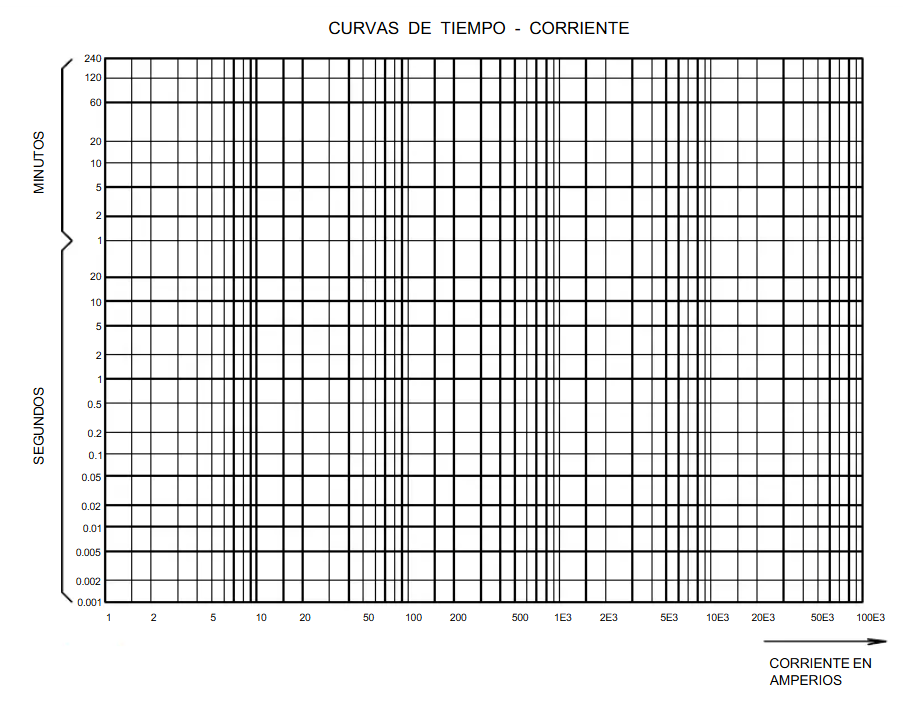
La escala logarítimica

La escala logarítmica es una forma de representar números y magnitudes que pueden abarcar un rango muy amplio, en una manera que sea más manejable y comprensible. En lugar de utilizar una escala lineal, donde cada incremento representa una cantidad fija, la escala logarítmica utiliza incrementos que representan factores multiplicativos.

Características de la escala logarítmica

1. Proporcionalidad Multiplicativa: En una escala logarítmica, moverse un cierto número de unidades a lo largo de la escala significa multiplicar el valor original por un número fijo. Por ejemplo, en una escala logarítmica base 10, moverse una unidad significa multiplicar el valor por 10.
2. Compresión de Rango: Esta escala es especialmente útil cuando se manejan datos que varían en órdenes de magnitud, como las intensidades de sonido, las magnitudes sísmicas o las concentraciones químicas. Permite representar de manera más compacta datos que varían ampliamente.

Ejemplo de escala logarítmica:

Imagina que estás graficando una escala logarítmica con base 10. Si tienes los números 1, 10, 100 y 1000, en una escala lineal, estos se verían muy dispersos. Sin embargo, en una escala logarítmica, se representarán como 0, 1, 2 y 3 respectivamente, haciendo la visualización más manejable.

Bases de los logaritmos

Los logaritmos pueden tener diferentes bases, y la elección de la base depende del contexto y de la aplicación específica. Aquí te presento los tipos de bases de logaritmos más comunes:

1. Logaritmo Decimal (Base 10)

El logaritmo en base 10, también conocido como logaritmo decimal o logaritmo común, es uno de los más utilizados. Se denota como log⁡₁₀(x) o simplemente log⁡(x) cuando la base está implícita.

Uso:

• Muy común en ingeniería y ciencias.
• Utilizado en la escala de Richter para medir la magnitud de terremotos y en la medida de intensidad del sonido (decibelios).

2. Logaritmo Natural (Base e)

El logaritmo natural tiene como base el número e (aproximadamente 2.71828), que es una constante matemática importante en cálculos exponenciales y logarítmicos. Se denota como log⁡_e(x) o más comúnmente como ln⁡(x).

Uso:

• Fundamental en cálculos de crecimiento exponencial y decaimiento.
• Amplio uso en matemáticas puras y en ciencias como la biología y la economía.

3. Logaritmo Binario (Base 2)

El logaritmo en base 2, conocido como logaritmo binario, se denota como log⁡₂(x).

Uso:

• Común en informática y teoría de la información.
• Usado en la evaluación de la complejidad de algoritmos y estructuras de datos.

4. Otras Bases Comunes

Aunque los logaritmos en base 10, base e y base 2 son los más comunes, los logaritmos pueden tener cualquier base positiva distinta de 1. Algunas bases específicas son utilizadas en contextos particulares:

• Base 3: Usado en ciertas aplicaciones de teoría de números.
• Base 5: Puede aparecer en problemas específicos de matemáticas discretas.

Cambios de Base

Una propiedad importante de los logaritmos es la capacidad de cambiar de una base a otra usando la fórmula:

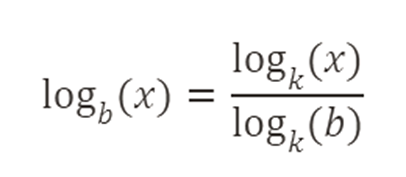
donde k puede ser cualquier base, comúnmente 10 o e.

Ejemplo Práctico

Si necesitas convertir un logaritmo de base 10 a base 2, puedes usar la fórmula:

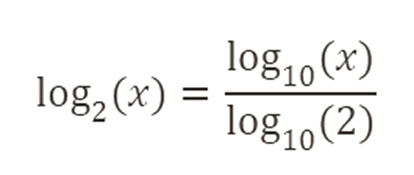
Esto facilita trabajar con diferentes bases según la aplicación.

Aplicaciones Comunes

1. Escala Richter: Utilizada para medir la magnitud de los terremotos, donde cada incremento de una unidad representa un aumento de 10 veces en la amplitud de las ondas sísmicas y aproximadamente 32 veces en la energía liberada.
2. Decibelios: En acústica, los niveles de sonido se miden en decibelios (dB). Un aumento de 10 dB representa un aumento de 10 veces en la intensidad del sonido.
3. Escala de pH: En química, el pH mide la acidez o alcalinidad de una solución y se define como el logaritmo negativo de la actividad de los iones hidrógeno (pH=−log⁡₁₀[H⁺]).
4. Magnitudes estelares: Los astrónomos usan la escala logarítmica para medir la luminosidad de las estrellas. Un cambio de una unidad en la magnitud representa un cambio de aproximadamente 2.5 veces en brillo.
5. Crecimiento Exponencial: En biología y economía, los logaritmos ayudan a modelar el crecimiento de poblaciones y el interés compuesto, donde las cantidades crecen multiplicativamente.

Resources:

---

Learning activities:

1. Caza del Tesoro Logarítmica

Materiales: Tarjetas con problemas de logaritmos, pistas escondidas por el aula.

Instrucciones:

• Divide a los estudiantes en equipos.
• Esconde tarjetas con problemas de logaritmos alrededor del aula.
• Cada tarjeta resuelta correctamente proporciona una pista para encontrar la siguiente.
• El primer equipo en completar todos los problemas y encontrar el tesoro gana un pequeño premio.

2. Carrera de Respuesta Rápida

Materiales: Pizarras blancas o pizarras individuales, marcadores.

Instrucciones:

• Formula una serie de preguntas rápidas sobre logaritmos.
• Los estudiantes, divididos en dos equipos, deben resolver cada problema lo más rápido posible en sus pizarras.
• El equipo que obtenga más respuestas correctas gana la carrera.

3. Bingo Logarítmico

Materiales: Tarjetas de bingo, fichas, lista de problemas y respuestas de logaritmos.

Instrucciones:

• Crea tarjetas de bingo con diferentes respuestas de problemas de logaritmos.
• Lee en voz alta problemas logarítmicos y los estudiantes deben resolverlos.
• Los estudiantes marcan las respuestas correctas en sus tarjetas de bingo.
• El primero en completar una fila (horizontal, vertical o diagonal) grita “¡Bingo!” y gana un premio.

4. Jenga Matemático

Materiales: Juego de Jenga, problemas de logaritmos escritos en los bloques.

Instrucciones:

• Escribe problemas de logaritmos en cada bloque de Jenga.
• Los estudiantes juegan Jenga y cada vez que sacan un bloque, deben resolver el problema de logaritmo en el bloque antes de colocarlo encima.
• Si resuelven mal, deben volver a colocar el bloque en su lugar original.

5. Escape Room Matemático

Materiales: Varios problemas de logaritmos, pistas, cronómetro.

Instrucciones:

• Organiza una actividad de “escape room” donde los estudiantes deben resolver problemas de logaritmos para avanzar a la siguiente pista.
• Coloca diferentes problemas en varias estaciones en el aula.
• Los estudiantes deben resolver cada problema para recibir la siguiente pista.
• El primer equipo en completar todas las estaciones y “escapar” del aula en el tiempo asignado gana.

Adaptaciones curriculares: