
¿Te has preguntado alguna vez cómo las matemáticas pueden ayudarnos a entender el mundo que nos rodea, desde la intensidad del sonido hasta el crecimiento de la población? Los logaritmos decimales y naturales son herramientas fundamentales en la ciencia, la ingeniería y las finanzas que nos permiten simplificar y resolver problemas complejos. En esta lección, exploraremos qué son los logaritmos decimales y naturales, sus ventajas, y cómo se utilizan en diferentes contextos.
Learning goals:
Al final de esta lección, tú serás capaz de:
- Comprender y diferenciar entre logaritmos decimales y naturales.
- Aplicar logaritmos decimales y naturales para simplificar expresiones y resolver ecuaciones.
- Identificar las ventajas principales de usar logaritmos decimales y naturales en diversos contextos.
- Resolver problemas prácticos utilizando logaritmos decimales y naturales.
- Reconocer aplicaciones de logaritmos en la vida diaria y en diferentes campos del conocimiento.
Logaritmos Decimales
Definición
Los logaritmos decimales, también conocidos como logaritmos comunes, tienen la base 10. Se denotan como log10(x) o simplemente log(x) cuando la base está implícita.
Ventajas
- Amplia Utilización: Utilizados en muchas aplicaciones prácticas, como la escala de Richter para medir terremotos y el cálculo de decibelios en acústica.
- Facilidad de Cálculo: Comunes en cálculos financieros y científicos, especialmente porque las calculadoras científicas y las herramientas de software a menudo tienen funciones específicas para logaritmos decimales.
- Escala Intuitiva: Facilitan la comparación de magnitudes que varían en órdenes de magnitud.
Logaritmos Naturales
Definición
Los logaritmos naturales tienen como base el número e (aproximadamente 2.71828). Se denotan como loge(x) o más comúnmente como ln(x).
Ventajas
- Relevancia Matemática: Son esenciales en el cálculo diferencial e integral, y en la modelación de procesos exponenciales y logarítmicos en la naturaleza.
- Cálculo Continuo: Utilizados en la derivación e integración de funciones exponenciales y logarítmicas.
- Aplicaciones Científicas: Comunes en biología, química y física para describir crecimiento exponencial, tasas de reacción, y leyes naturales.
Ejercicios de Ejemplo



Resources:
Learning activities:
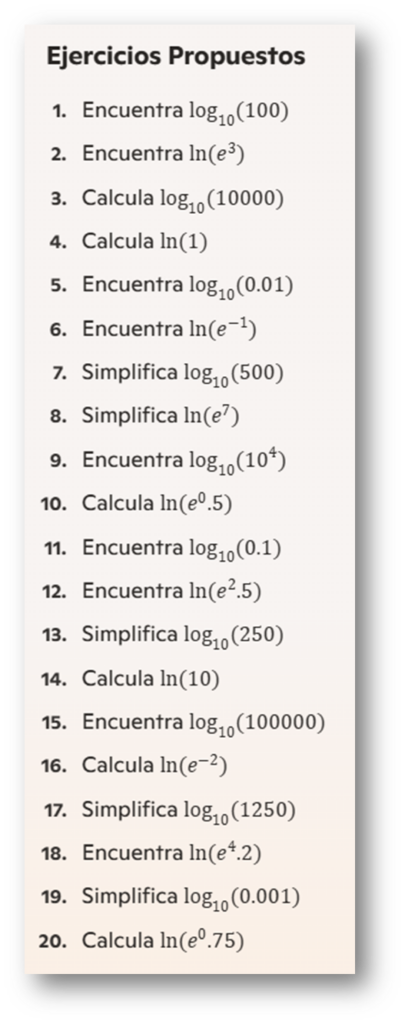
Actividades Lúdicas para el Aula
- Rompecabezas de Logaritmos:
- Divide a la clase en grupos y proporciona piezas de rompecabezas con problemas de logaritmos decimales y naturales y sus soluciones. Los estudiantes deben unir correctamente las piezas para completar el rompecabezas.
- Bingo de Logaritmos:
- Crea tarjetas de bingo con diferentes problemas de logaritmos decimales y naturales. A medida que se lean los problemas, los estudiantes deben resolverlos y marcar las respuestas correctas en sus tarjetas de bingo.
- Carrera de Logaritmos:
- Organiza una carrera donde los estudiantes, en equipos, deben resolver problemas de logaritmos decimales y naturales lo más rápido posible. Proporciona puntos por cada respuesta correcta y premia al equipo con más puntos.
- Jenga Matemático de Logaritmos:
- Usa un juego de Jenga donde cada bloque tenga un problema de logaritmos decimales o naturales escrito. Los estudiantes deben resolver el problema antes de apilar el bloque en la torre.
- Escape Room de Logaritmos:
- Crea una serie de pistas y problemas de logaritmos decimales y naturales que los estudiantes deben resolver para avanzar a la siguiente pista y finalmente “escapar” del aula. Divide a los estudiantes en equipos y dales un tiempo límite para completar todas las pistas.
Adaptaciones curriculares:
Resolver la mitad o cuarta parte de los ejercicios propuestos.
