
¿Te has encontrado alguna vez con problemas matemáticos que parecen imposibles de resolver? Las ecuaciones logarítmicas son una de esas joyas matemáticas que, con las herramientas y técnicas adecuadas, se vuelven manejables y hasta divertidas. Estas ecuaciones juegan un papel crucial en muchos campos, desde la ciencia hasta la economía, y te permitirán explorar y resolver problemas complejos de manera eficiente. Prepárate para desbloquear el poder de los logaritmos y llevar tus habilidades matemáticas al siguiente nivel.
Learning goals:
Al final de esta lección, tú serás capaz de:
- Comprender qué son las ecuaciones logarítmicas y sus aplicaciones.
- Identificar y aplicar las propiedades de los logaritmos para resolver ecuaciones logarítmicas.
- Utilizar técnicas de resolución paso a paso para solucionar ecuaciones logarítmicas.
- Reconocer y corregir errores comunes al trabajar con ecuaciones logarítmicas.
- Aplicar ecuaciones logarítmicas en contextos prácticos y situaciones de la vida diaria.
Recomendaciones para la resolución de ejercicios
- Comprender las Propiedades de los Logaritmos: Familiarízate con las propiedades básicas de los logaritmos, como la propiedad del producto, la propiedad del cociente y la propiedad de la potencia.
- Simplificar la Ecuación: Utiliza las propiedades de los logaritmos para simplificar la ecuación logarítmica antes de intentar resolverla.
- Cambiar de Forma Logarítmica a Exponencial: En muchos casos, es útil cambiar la ecuación de su forma logarítmica a una forma exponencial.
- Resolver para la Variable: Una vez que la ecuación esté simplificada, resuelve para la variable desconocida.
- Verificar la Solución: Sustituye la solución encontrada en la ecuación original para asegurarte de que es correcta.
Técnicas de Resolución de Ecuaciones Logarítmicas
- Usar las Propiedades del Logaritmo:
- Propiedad del Producto: logb(MN)=logb(M)+logb(N)
- Propiedad del Cociente: logb(MN)=logb(M)−logb(N)
- Propiedad de la Potencia: logb(Mk)=k logb(M)
- Cambio de Base:
- Utiliza la fórmula de cambio de base:
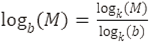
- Utiliza la fórmula de cambio de base:
- Convertir a Forma Exponencial:
- Cambia una ecuación logarítmica a forma exponencial para facilitar la resolución.
Ejemplos:





Ejemplos de Ecuaciones Logarítmicas con Coeficientes y Logaritmos en Ambos Lados





Resources:
Learning activities:
Ejercicios Propuestos


Actividades Lúdicas para el Aula
- Rompecabezas de Ecuaciones Logarítmicas:
- Divide a la clase en grupos y proporciona piezas de rompecabezas con ecuaciones logarítmicas y sus soluciones. Los estudiantes deben unir correctamente las piezas para completar el rompecabezas.
- Bingo de Ecuaciones Logarítmicas:
- Crea tarjetas de bingo con diferentes ecuaciones logarítmicas. A medida que se leen las ecuaciones, los estudiantes deben resolverlas y marcar las respuestas correctas en sus tarjetas de bingo.
- Carrera de Ecuaciones Logarítmicas:
- Organiza una carrera donde los estudiantes, en equipos, deben resolver ecuaciones logarítmicas lo más rápido posible. Proporciona puntos por cada respuesta correcta y premia al equipo con más puntos.
- Jenga Matemático de Ecuaciones Logarítmicas:
- Usa un juego de Jenga donde cada bloque tenga un problema de ecuaciones logarítmicas escrito. Los estudiantes deben resolver el problema antes de apilar el bloque en la torre.
- Escape Room de Ecuaciones Logarítmicas:
- Crea una serie de pistas y problemas de ecuaciones logarítmicas que los estudiantes deben resolver para avanzar a la siguiente pista y finalmente “escapar” del aula. Divide a los estudiantes en equipos y dales un tiempo límite para completar todas las pistas.
Adaptaciones curriculares:
Resolver la mitad o la cuarta parte de los ejercicios propuestos.
