
Aclaremos algo: ¿Qué es un escalar?
Un escalar es un concepto fundamental en matemáticas y física que representa una cantidad con solo magnitud y no tiene dirección. A diferencia de los vectores, que tienen tanto magnitud como dirección, los escalares están completamente definidos por un valor numérico.
Características de los escalares:
- Magnitud: Tienen una magnitud que puede ser positiva, negativa o cero.
- Independencia Direccional: No tienen dirección asociada. Por ejemplo, la temperatura y la masa son cantidades escalares porque solo necesitas un valor numérico para describirlas.
- Operaciones: Puedes sumar, restar, multiplicar y dividir escalares de manera simple. Por ejemplo, si tienes dos masas, puedes sumarlas directamente para obtener la masa total.
Ejemplos de escalares:
- Temperatura: 25°C o 77°F.
- Tiempo: 10 segundos.
- Longitud: 5 metros.
- Volumen: 3 litros.
Multiplicación de un escalar por un vector
Multiplicar un escalar por un vector implica escalar (ajustar el tamaño) del vector original por un valor dado. Si tienes un escalar k y un vector v=(v1,v2), el resultado de la multiplicación es un nuevo vector (k⋅v1,k⋅v2). Básicamente, multiplicas cada componente del vector original por el escalar.
Ejemplo gráfico:
Pongamos el siguiente vector A:

Si multiplicamos el escalar 3 por el vector A, es decir, 3A, obtenemos un nuevo vector en la misma dirección de A, pero de tres veces el tamaño de A, así:
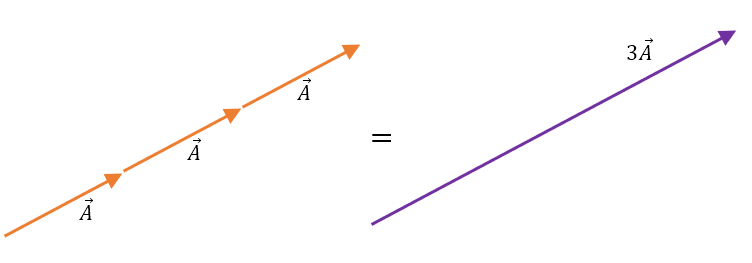
Además, si el escalar fuera un valor negativo, por ejemplo, -2, entonces -2A equivale a dos veces el vector A, pero en sentido contrario, así:
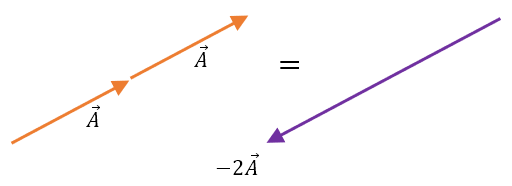
De forma analítica
De forma analítica, si el vector está expresado en coordenadas polares o geográficas:
- Si el escalar es un número positivo, nada más se multiplica por el módulo. El ángulo queda intacto.
- Si el escalar es un número negativo, suceden dos cosas: 1. se multiplica por el módulo (pero debe dejarse el nuevo módulo resultante como positivo), y 2. El ángulo en coordenadas geográficas es el mismo, y solo cambian los puntos cardinales por sus opuestos. En cambio, el ángulo en coordenadas polares debe sumar o restar 180° (cualquiera de las dos operaciones que me dé como resultado un nuevo ángulo positivo).
Ejemplo1:
- Escalar: k=3
- Vector Polar Original: v=(r=5,θ=45°)
- Resultado: k⋅v = (3 ⋅ 5, 45°) = (15, 45°)
- Interpretación: El nuevo vector tiene una magnitud de 15 y el mismo ángulo de 45 grados.
Ejemplo 2:
Supongamos que tenemos un vector de desplazamiento en coordenadas geográficas:
- Vector Original: (50 km, N 45° E).
- Escalar: k=−2.
Al multiplicar el vector por el escalar negativo:
- Nueva Magnitud: 2 ⋅ 50 km = 100 km
- Nueva Dirección: S 45° O (cambian los puntos cardinales por sus opuestos)
- Resultado: El nuevo vector sería un desplazamiento de 100100 km en dirección 225∘225^\circ (o sea, 45 grados Suroeste).
- Interpretación: El vector original de 50 km hacia 45 grados Noreste se transforma en un vector de 100 km y 45 grados Suroeste al multiplicarlo por -2.
De forma analítica, si el vector está expresado en coordenadas rectangulares:
- Simplemente se multiplica el escalar con cada uno de los componentes (x y y), es decir, de forma distributiva, obteniéndose un vector con nuevas componentes x y y. No hay que olvidar la ley de signos.
Ejemplos:
Escalar y vector:
- Escalar: k=3
- Vector: v=(2,4)
- Resultado: 3 ⋅ v = (3 ⋅ 2, 3 ⋅ 4) = (6,12)
Escalar negativo y vector:
- Escalar: k=−2
- Vector: v=(5,−3)
- Resultado: −2 ⋅ v = (−2 ⋅ 5, −2 ⋅ (−3)) = (−10,6)
