
¿Alguna vez te has preguntado cómo los matemáticos resuelven misterios? ¡Bienvenido al mundo de las ecuaciones e inecuaciones de dos variables! Imagina que eres un detective en busca de pistas entre los números, resolviendo enigmas que pueden ayudarte a entender desde la economía hasta la ingeniería. ¡Sí, todo comienza con dos simples variables y sus ecuaciones!
Las ecuaciones e inecuaciones no son solo problemas en un papel. Son herramientas poderosas que nos permiten modelar situaciones de la vida real, encontrar soluciones a problemas complejos y prever resultados futuros. En esta lección, aprenderás a manipular estos términos como un maestro y descubrirás el increíble mundo matemático que te rodea. ¡Prepárate para una aventura llena de números y lógica!
Learning goals:
- Comprender la definición y estructura de ecuaciones e inecuaciones de dos variables.
- Resolver ecuaciones lineales y no lineales de dos variables.
- Representar gráficamente ecuaciones e inecuaciones de dos variables.
- Analizar y discutir las soluciones obtenidas de las ecuaciones e inecuaciones.
- Aplicar ecuaciones e inecuaciones de dos variables a problemas del mundo real.
Métodos de solución de sistemas de ecuaciones lineales de dos incógnitas
Método de sustitución
Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.
Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.
Para el Método de Sustitución, procederemos así:
- Escogemos una ecuación y una incógnita.
- Despejamos esa incógnita de la ecuación escogida (es decir, la dejamos sola de un lado de la ecuación)
- Reemplazamos la expresión despejada de esta incógnita en la misma incógnita pero de la otra ecuación (de esta manera, obtendremos una ecuación con una sola incógnita)
- Despejamos esa incógnita y obtendremos su valor. Ya tenemos el valor de una de ellas.
- Colocamos el valor obtenido de esta incógnita en cualquier otra ecuación, la despejamos y obtenemos el valor de la otra incógnita.
Ejemplo:
Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.
Sitema:
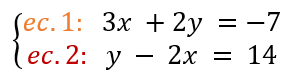
Seguimos las reglas:
- Escogemos una ecuación y una incógnita. Escogeré, por ejemplo, la ecuación 1 (ec. 1), y de ella la incógnita “y“.
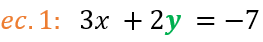
- Despejamos esa incógnita de la ecuación escogida (es decir, la dejamos sola de un lado de la ecuación). Siguiendo el procedimiento de despeje de ecuaciones, al despajar “y” obtenemos una nueva ecuación (ec. 1.1) así:
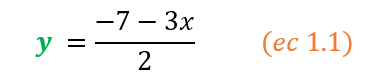
- Reemplazamos la expresión despejada de esta incógnita “y” (de la ec. 1.1) en la misma incógnita “y“ pero de la otra ecuación del sistema (ec. 2). De esta manera, obtendremos una nueva ecuación (ec. 2.1) con una sola incógnita, la incógnita “x”. Veámoslo así:
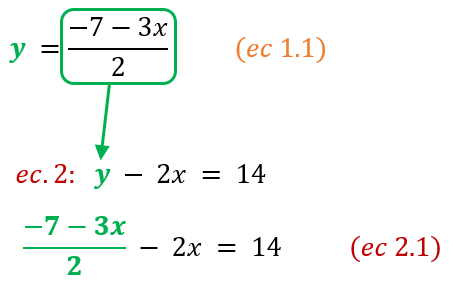
- Despejamos esa incógnita “x” y obtendremos su valor. Con ello, ya tendríamos el valor de una de ellas, en este caso, de “x”.
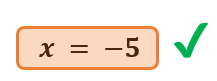
- Colocamos el valor obtenido de esta incógnita “x” en cualquier otra ecuación, por ejemplo, en la ecuación “ec. 1.1”, con la cual, al efectuar los cálculos respectivos, obtenemos el valor de la otra incógnita.

¡Y listo!
Podemos presentar la solución como un conjunto:
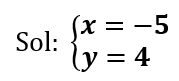
Método de reducción
Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.
Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.
Para el Método de Reducción, procederemos así:
- Multiplicar para igualar coeficientes. Ajusta una o ambas ecuaciones multiplicándolas por los factores necesarios para que los coeficientes de una de las incógnitas sean iguales (pero de signo contrario).
- Sumar o restar las ecuaciones. Combina las ecuaciones sumando o restando para eliminar una de las incógnitas, obteniendo así una nueva ecuación con una sola incógnita.
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda.
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones originales para encontrar el valor de la otra incógnita.
Ejemplo:
Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.
Sistema:
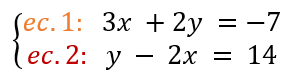
Seguimos las reglas:
- Multiplicar para igualar coeficientes. Ajusta una o ambas ecuaciones multiplicándolas por los factores necesarios para que los coeficientes (los números que multiplican con las letras) de una de las incógnitas sean iguales (pero de signo contrario). Para más facilidad, ordenemos las ecuaciones.
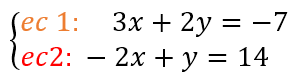
Ahora, escogemos eliminar una de las incógnitas. En nuestro ejemplo, escogeremos eliminar “y”. Para ello, debemos lograr que los coeficientes que acompañan a “y” en cada ecuación sean iguales, pero de signos contrarios. El la primera ecuación, el coeficiente que acompaña a “y” es 2, y en la segunda ecuación, el coeficiente que acompaña a “y” es 1. Debemos multiplicar un valor al coeficiente 2 de la primera ecuación, y otro valor al coeficiente 1 de la segunda ecuación para lograr que sean iguales con signos contrarios. ¿Qué valores usarías?
Por ejemplo, a 2 de la primera ecuación podría multiplicarlo por 3, entonces 2x3=6.
Entonces, a 1 de la segunda ecuación debería multiplicarlo por -6, entonces 1x(-6)=-6
Como puedes ver, ahora logramos que tengan el mismo valor, pero con signos contrarios. En nuestro ejemplo, logramos obtener 6 y -6.
Entonces, el valor que debemos multiplicar a la primera ecuación es 3 y a la segunda ecuación es -6. De esta forma los coeficientes de la incógnita “y” que queremos eliminar serán iguales pero de signo contrario, 6 y -6. Al multiplicar los valores por cada ecuación, aplicaremos la propiedad distributiva (no olvidemos la ley de signos):
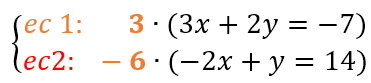
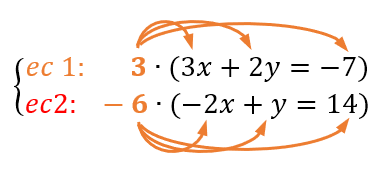
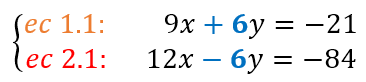
- Sumar o restar las ecuaciones. Combina las ecuaciones sumando o restando para eliminar una de las incógnitas, obteniendo así una nueva ecuación con una sola incógnita. En nuestro ejemplo, sumamos “x” con “x”, y al operar “y” con “y”, esta se elimina debido a que sus coeficientes se neutralizan. También debemos sumar los valores del otro lado de las ecuaciones. Así:
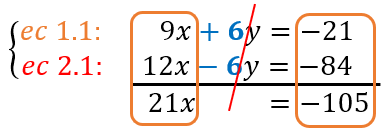
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda. Como puedes ver, la nueva ecuación obtenida (ec. 3) es:
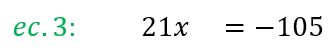
Al despejar “x” obtenemos:
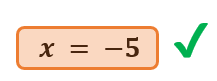
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones originales para encontrar el valor de la otra incógnita. Para nuestro ejemplo, sustituiremos el valor de “x=-5” en la ecuación 1:

¡Y listo!
Podemos presentar la solución como un conjunto:
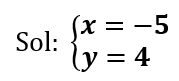
Método de igualación
Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.
Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.
Para el Método de Reducción, procederemos así:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones.
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación.
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda.
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita.
Ejemplo:
Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.
Sistema:
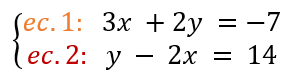
Seguimos las reglas:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones. Para nuestro ejemplo, vamos a despejar “y” de ambas ecuaciones:
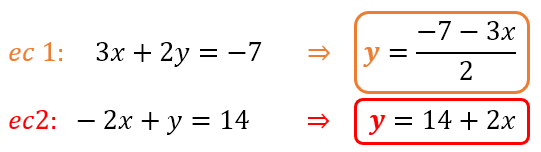
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación. Como despejamos “y” de ambas ecuaciones, y dado que “y=y”, reemplazamos los valores de esta en una nueva ecuación (ec. 3):
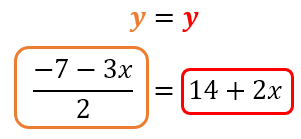
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda, que en este caso, es “x”.
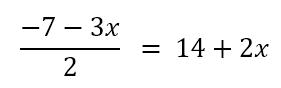
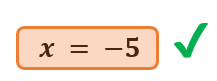
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita. En nuestro caso, podemos sustituirlas incluso en cualquiera de las dos ecuaciones despejadas anteriormente. Por facilidad, escojamos reemplazar el valor de x=-5 en la ecuación que anteriormente encerramos en rojo:
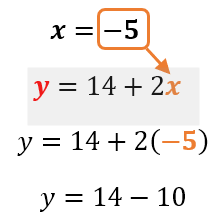

¡Y listo!
Podemos presentar la solución como un conjunto:
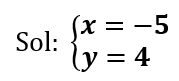
Método gráfico
Imaginemos los sistemas de ecuaciones como un juego con reglas. Si las seguimos, llegaremos ciertamente a la respuesta. El objetivo es encontrar el valor de cada variable.
Nota: Usaremos sistemas de dos ecuaciones con dos incógnitas.
Para el Método de Reducción, procederemos así:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones.
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación.
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda.
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita.
Ejemplo:
Resolvamos el siguiente sistema de dos ecuaciones con dos incógnitas. Para entender el uso de las ecuaciones en el procedimiento, usaremos por ejemplo “ec. 1” que significa “ecuación 1”; así mismo, de ecuaciones obtenidas a partir de otras, como por ejemplo, “ec. 4.1” y “ec. 4.2” que significa que de la ecuación 4 se obtuvieron dos ecuaciones más a las que hemos numerado 4.1 y 4.2.
Sistema:
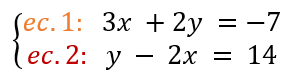
Seguimos las reglas:
- Despejar una misma incógnita. Escogemos una incógnita y la despejamos de ambas ecuaciones. Para nuestro ejemplo, vamos a despejar “y” de ambas ecuaciones:
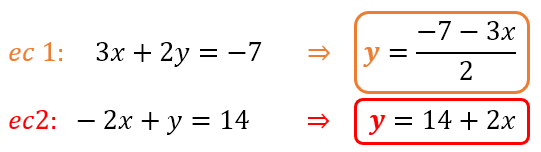
- Igualamos los valores de las incógnitas despejadas. En el lado izquierdo ponemos el valor de la incógnita despejada de una de las ecuaciones, y en el lado derecho colocamos el valor de la incógnita despejada de la otra ecuación. Como despejamos “y” de ambas ecuaciones, y dado que “y=y”, reemplazamos los valores de esta en una nueva ecuación (ec. 3):
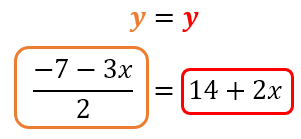
- Resolver la nueva ecuación. Resuelve la ecuación obtenida en el paso anterior para encontrar el valor de la incógnita que queda, que en este caso, es “x”.
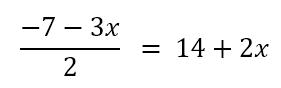
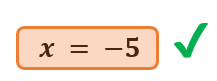
- Sustituir y resolver. Sustituye el valor encontrado en cualquiera de las ecuaciones para encontrar el valor de la otra incógnita. En nuestro caso, podemos sustituirlas incluso en cualquiera de las dos ecuaciones despejadas anteriormente. Por facilidad, escojamos reemplazar el valor de x=-5 en la ecuación que anteriormente encerramos en rojo:
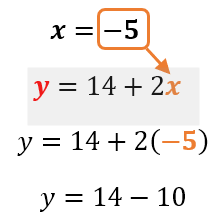

¡Y listo!
Podemos presentar la solución como un conjunto:
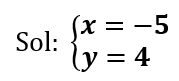
Regla de Cramer
Determinantes
Regla de Cramer
Inecuaciones de dos variables
Se representan en el plano cartesiano, como una región sombreada bajo la ecuación lineal correspondiente.
Para graficar una inecuación lineal de dos variables, debes seguir una serie de pasos y condiciones. Aquí están las reglas básicas:
- Escribe la inecuación en forma estándar: La inecuación debe estar en una forma similar a ax+by≤c, ax+by≥c, ax+by<c, o ax+by>c.
- Dibuja la línea límite:
- Si la inecuación es ≤ o ≥, dibuja una línea sólida.
- Si la inecuación es < o >, dibuja una línea punteada.
- Esta línea representa la ecuación ax+by=c.
- Encuentra los puntos de intersección:
- Si y está aislado, puedes encontrar fácilmente puntos específicos para x y y sustituyendo valores.
- Otra manera es identificar los puntos donde la línea cruza los ejes x y y (cuando x=0 y y=0).
- Determina la región de la solución:
- Elige un punto de prueba que no esté en la línea límite (a menudo el punto (0,0) es una elección conveniente si no está sobre la línea).
- Sustituye este punto en la inecuación original.
- Si la inecuación es verdadera, la región donde está ese punto es la solución.
- Si la inecuación es falsa, la solución está en la región opuesta a ese punto.
- Sombrear la región de solución:
- Sombrea la región que contiene todos los puntos que satisfacen la inecuación.
- Esta área es donde se encuentran todas las soluciones de la inecuación.

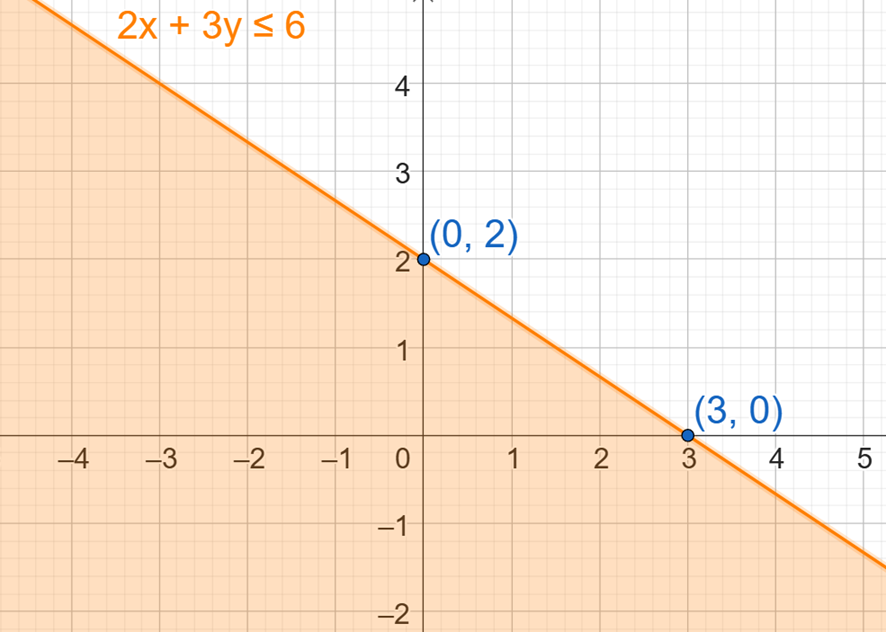
La gráfica correspondiente del ejemplo anterior es:
Sistemas de inecuaciones de dos variables
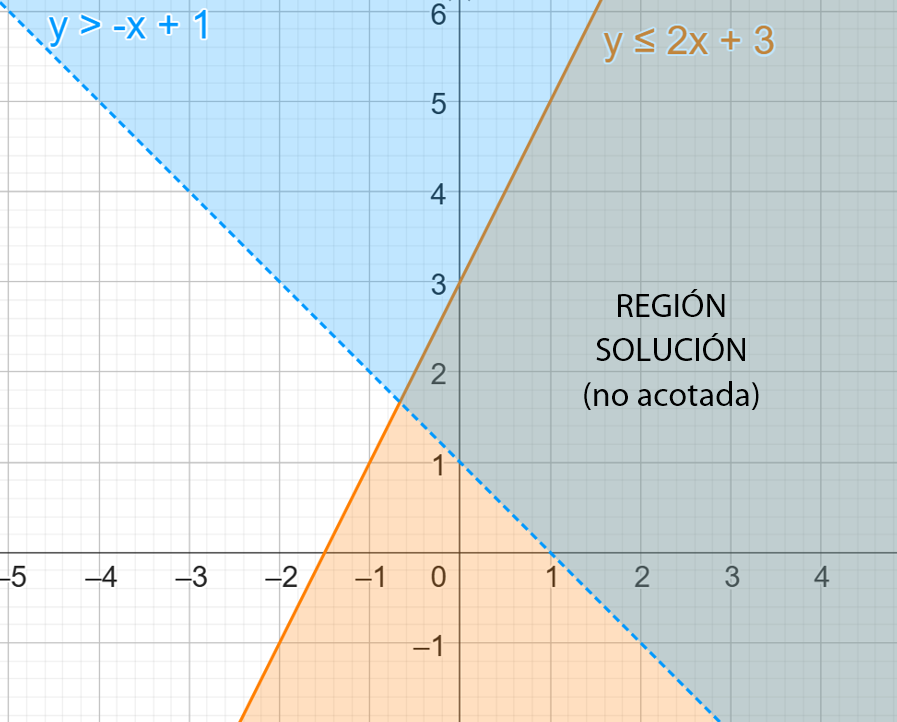
Los sistemas de inecuaciones de dos variables son conjuntos de inecuaciones de dos variables que se representan en el plano, y cuyas regiones sombreadas se cruzan o sobreponen en una sola región llamada región solución, misma que puede ser acotada si la región es un polígono (cerrado), o no acotada si la región está abierta por un lado y se expande de forma infinita.
Cada ecuación se grafica en el mismo plano cartesiano como se indicó en el ejemplo anterior.

La gráfica solución del ejemplo anterior es:
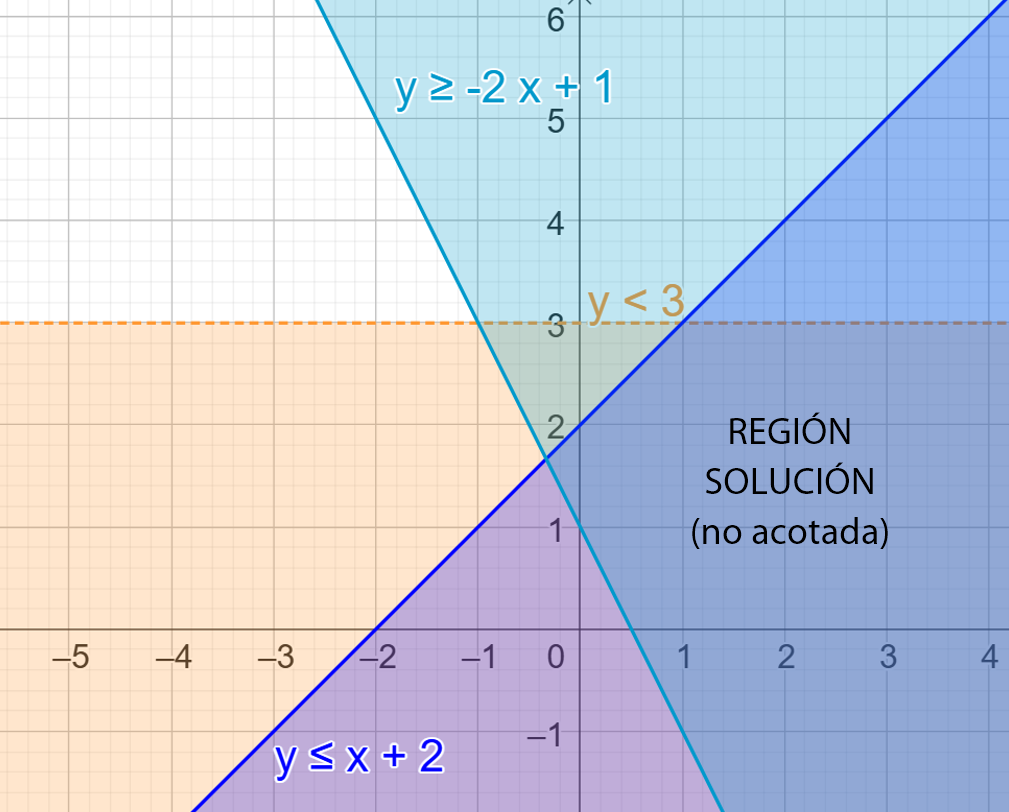
Ejemplo 2:

La gráfica de las ecuaciones es:
Resources:
Learning activities:
Adaptaciones curriculares:
–
–
–
–
