Análisis de datos para datos agrupados

El análisis de datos agrupados es una técnica fundamental en estadística que permite organizar y resumir grandes conjuntos de datos en intervalos o clases. Este enfoque facilita la interpretación de datos y la extracción de conclusiones significativas. En esta lección, aprenderás a realizar análisis de datos agrupados, comprenderás las fórmulas necesarias y explorarás ejemplos prácticos para aplicar estos conceptos en situaciones reales.

---

Learning goals:

• Comprender el concepto de datos agrupados y su importancia en el análisis estadístico.
• Identificar y definir intervalos de clase para organizar conjuntos de datos grandes.
• Calcular medidas estadísticas clave (como la media, mediana y moda) para datos agrupados.
• Analizar la dispersión de los datos mediante el cálculo de varianza y desviación estándar.
• Aplicar las fórmulas y técnicas aprendidas en ejemplos prácticos para reforzar la comprensión.

---

Ejemplo 1: Análisis de Datos Agrupados

Paso 1: Definir Intervalos de Clase

Supongamos que tenemos un conjunto de datos con edades de 50 personas:

20, 22, 23, 24, 25, 25, 26, 27, 27, 28, 28, 29, 30, 30, 30, 31, 32, 33, 34, 35,
35, 36, 37, 38, 39, 40, 40, 41, 42, 43, 44, 45, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60

Dividimos los datos en intervalos de clase de 5 unidades:

• 20-24
• 25-29
• 30-34
• 35-39
• 40-44
• 45-49
• 50-54
• 55-59
• 60-64

Paso 2: Construir la Tabla de Frecuencia

Intervalo	Frecuencia	Marca de Clase (x)	Frecuencia Relativa (f)	f * x
20-24	4	22	0.08	1.76
25-29	6	27	0.12	3.24
30-34	5	32	0.10	3.20
35-39	5	37	0.10	3.70
40-44	5	42	0.10	4.20
45-49	5	47	0.10	4.70
50-54	6	52	0.12	6.24
55-59	7	57	0.14	7.98
60-64	7	62	0.14	8.68
Total	50		1.00	43.70

Medidas de Tendencia Central

Paso 3: Calcular la Media

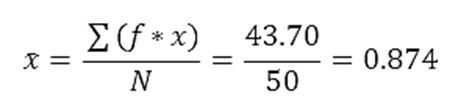
Paso 4: Calcular la Mediana

• Localizamos la posición de la mediana:

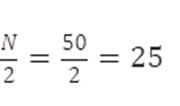
• La mediana está en el intervalo 30-34.
• Aplicando la fórmula:

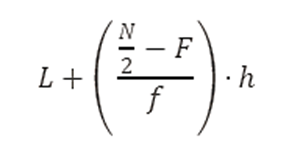
• L = límite inferior del intervalo de la mediana = 30
• F = frecuencia acumulada antes del intervalo de la mediana = 10
• f = frecuencia del intervalo de la mediana = 5
• h = tamaño del intervalo = 5

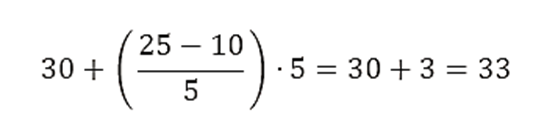
Paso 5: Calcular la Moda

• El intervalo modal es 55-59, ya que tiene la mayor frecuencia.
• Aplicando la fórmula de la moda para datos agrupados:

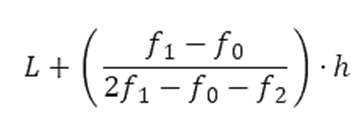
• L = límite inferior del intervalo modal = 55
• f₁ = frecuencia del intervalo modal = 7
• f₀ = frecuencia del intervalo anterior al modal = 6
• f₂ = frecuencia del intervalo siguiente al modal = 6

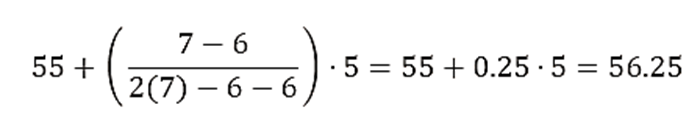
Medidas de Dispersión

Paso 6: Calcular la Varianza

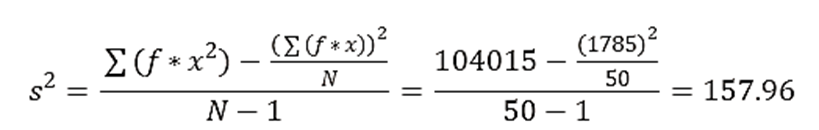
Paso 7: Calcular la Desviación Estándar

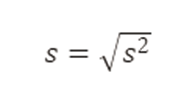
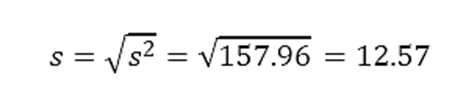
Medidas de posición

Medidas de Posición

Paso 8: Percentil (P_k)

• Para calcular el percentil 25 (P₂₅):

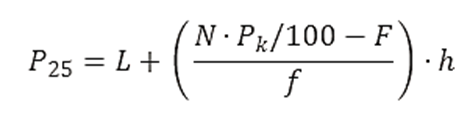
• L = 20
• N⋅P_k/100 = 50⋅0.25=12.5
• F = 4
• f = 6
• h = 5

---

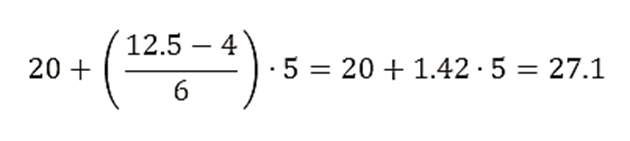
Ejemplo 2: Análisis de Datos Agrupados en Alturas

Paso 1: Definir Intervalos de Clase

Supongamos que tenemos un conjunto de datos con alturas (en cm) de 40 personas:

150, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170,
171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190

Dividimos los datos en intervalos de clase de 5 unidades:

• 150-154
• 155-159
• 160-164
• 165-169
• 170-174
• 175-179
• 180-184
• 185-189
• 190-194

Paso 2: Construir la Tabla de Frecuencia

Intervalo	Frecuencia	Marca de Clase (x)	Frecuencia Relativa (f)	f * x
150-154	5	152	0.125	19.00
155-159	5	157	0.125	19.625
160-164	5	162	0.125	20.25
165-169	5	167	0.125	20.875
170-174	5	172	0.125	21.50
175-179	5	177	0.125	22.125
180-184	5	182	0.125	22.75
185-189	5	187	0.125	23.375
190-194	5	192	0.125	24.00
Total	40		1.00	173.50

Medidas de Tendencia Central

Paso 3: Calcular la Media

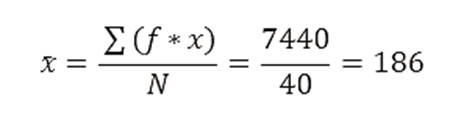
Paso 4: Calcular la Mediana

• Localizamos la posición de la mediana:

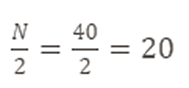
• La mediana está en el intervalo 165-169.
• Aplicando la fórmula:

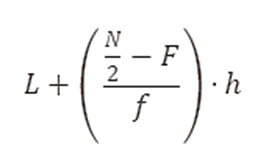
• L = 165
• F = 15
• f = 5
• h = 5

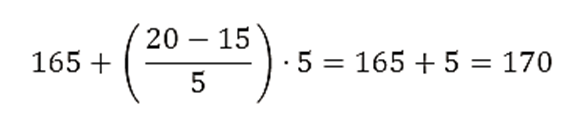
Paso 5: Calcular la Moda

• El intervalo modal es 150-154, ya que tiene la mayor frecuencia.
• Aplicando la fórmula de la moda para datos agrupados:

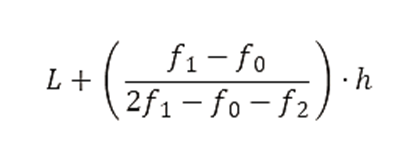
• f₁ = frecuencia del intervalo modal = 5
• f₀ = frecuencia del intervalo anterior al modal = 5
• f₂ = frecuencia del intervalo siguiente al modal = 5

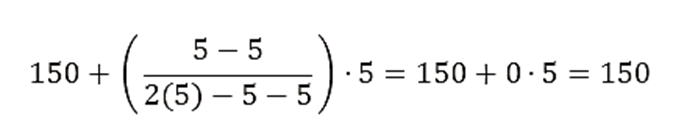
Medidas de Dispersión

Paso 6: Calcular la Varianza

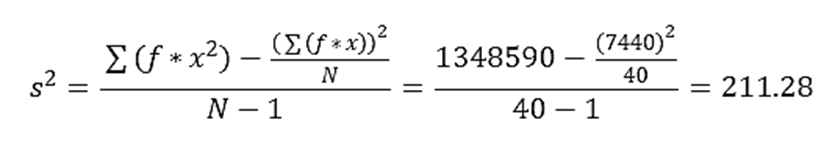
Paso 7: Calcular la Desviación Estándar

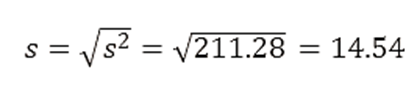
Medidas de posición

Percentil (P_k)

• Para calcular el percentil 25 (P₂₅):

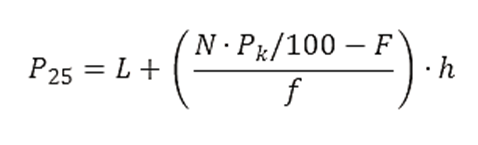
• L = 150
• N⋅P_k/100=40⋅0.25=10
• F = 5
• f = 5
• h = 5

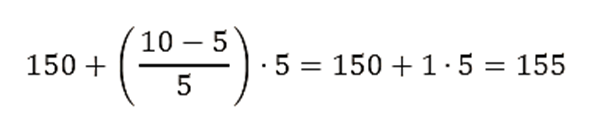
• Para calcular el percentil 75 (P₇₅):

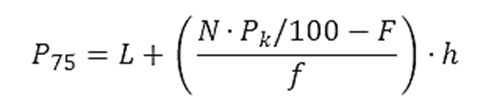
• L = 180
• N⋅P_k/100=40⋅0.75=30
• F = 25
• f = 5
• h = 5

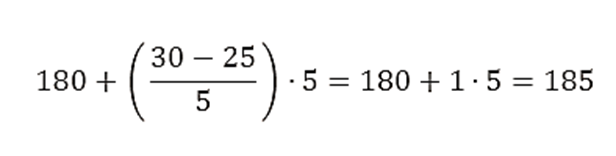
Deciles (D_k)

• Para calcular el decil 1 (D₁):

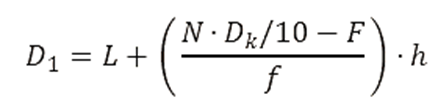
• L = 150
• N⋅D_k/10=40⋅0.1=4
• F = 0
• f = 5
• h = 5

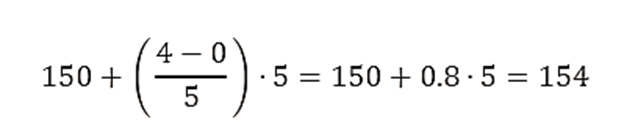
• Para calcular el decil 9 (D₉):

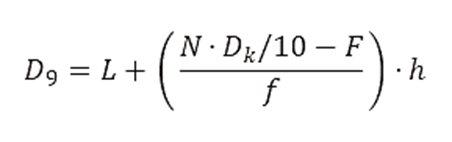
• L = 185
• N⋅D_k/10=40⋅0.9=36
• F = 35
• f = 5
• h = 5

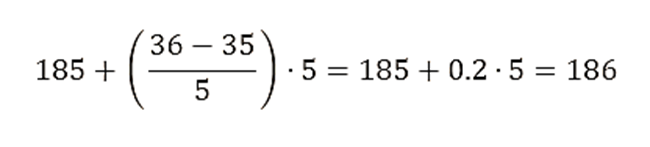
Resources:

---

Learning activities:

Ejercicio 1: Análisis de Datos de Pesos

Datos

Supongamos que tenemos los siguientes datos de pesos (en kg) de 50 personas:

58, 60, 61, 62, 63, 65, 66, 68, 69, 70,
71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
58, 59, 61, 63, 65, 67, 68, 70, 71, 72,
73, 75, 76, 78, 79, 80, 82, 83, 85, 86,
87, 88, 89, 90, 91, 92, 93, 94, 95, 96

Instrucciones

1. Definir los intervalos de clase: Divide los datos en intervalos de clase apropiados.
2. Construir la tabla de frecuencia: Incluye la frecuencia absoluta, frecuencia relativa y acumulada.
3. Calcular la media, mediana y moda.
4. Calcular la varianza y desviación estándar.
5. Calcular el percentil 25 y percentil 75.

---

Ejercicio 2: Análisis de Datos de Temperaturas

Datos

Supongamos que tenemos los siguientes datos de temperaturas diarias (en °C) registradas durante 30 días:

23, 24, 24, 25, 25, 26, 27, 28, 28, 29,
29, 30, 30, 31, 31, 32, 32, 33, 34, 34,
23, 23, 24, 26, 27, 27, 29, 30, 31, 32

Instrucciones

1. Definir los intervalos de clase: Divide los datos en intervalos de clase apropiados.
2. Construir la tabla de frecuencia: Incluye la frecuencia absoluta, frecuencia relativa y acumulada.
3. Calcular la media, mediana y moda.
4. Calcular la varianza y desviación estándar.
5. Calcular el decil 1 y decil 9.

---

Consejos

• Intervalos de Clase: Recuerda que los intervalos de clase deben ser mutuamente excluyentes y exhaustivos.
• Frecuencia Relativa: Es el cociente entre la frecuencia absoluta y el total de datos.
• Frecuencia Acumulada: Es la suma de las frecuencias absolutas hasta un determinado intervalo.
• Medidas de Tendencia Central y Dispersión: Utiliza las fórmulas específicas para datos agrupados.
• Medidas de Posición: Los percentiles y deciles ayudan a entender la distribución de los datos dentro del conjunto.

Adaptaciones curriculares:

Ejercicio Propuesto: Análisis de Datos Sencillos

Datos

Supongamos que tenemos los siguientes datos sobre las edades de 10 estudiantes en una clase:

10, 12, 11, 10, 12, 11, 13, 10, 12, 11

Instrucciones

1. Organiza los datos: Coloca los datos en una tabla sencilla.
2. Calcula la Frecuencia: Cuenta cuántas veces aparece cada edad.
3. Encuentra la Edad que Más se Repite: Identifica cuál es la edad que se repite más veces (moda).

Tabla de Frecuencia

Edad	Frecuencia
10	3
11	3
12	3
13	1

Respuestas

1. Organiza los datos:10, 12, 11, 10, 12, 11, 13, 10, 12, 11
2. Calcula la Frecuencia: Ya está calculada en la tabla de frecuencia arriba.
3. Encuentra la Edad que Más se Repite (Moda): La moda es 10, 11 y 12, ya que estas edades se repiten 3 veces cada una.