Estrategias de resolución de problemas

La resolución de problemas en estadística no solo implica aplicar fórmulas y ejecutar cálculos, sino también desarrollar un pensamiento crítico y estratégico. Esta lección te proporcionará las herramientas necesarias para abordar problemas estadísticos de manera estructurada y eficiente, convirtiendo datos complejos en información comprensible y accionable.

---

Learning goals:

• Desarrollar habilidades para identificar y definir problemas estadísticos de manera precisa.
• Aplicar estrategias adecuadas para descomponer problemas complejos en pasos más manejables.
• Seleccionar y utilizar herramientas estadísticas y técnicas de análisis de datos efectivas.
• Interpretar resultados estadísticos con claridad y precisión para tomar decisiones informadas.
• Presentar soluciones y resultados de manera coherente y comprensible, utilizando gráficos y tablas.

---

Estrategias de Resolución de Problemas

1. Identificación y Definición del Problema

Primero, es crucial comprender completamente el problema que estás tratando de resolver. Define claramente el objetivo del análisis estadístico y determina qué datos necesitarás.

Ejemplo: Supongamos que deseas analizar las calificaciones de un grupo de estudiantes para determinar si existe una relación entre las horas de estudio y las calificaciones obtenidas. El problema está definido como: “¿Existe una correlación entre las horas de estudio y las calificaciones de los estudiantes?”

2. Recolección y Organización de Datos

Reúne los datos necesarios y organízalos en una forma estructurada, como una tabla o una hoja de cálculo. Asegúrate de que los datos sean precisos y completos.

Ejemplo: Recopila datos de 10 estudiantes que incluyen las horas de estudio y sus calificaciones:

Estudiante	Horas de Estudio	Calificación
1	5	85
2	6	88
3	4	78
4	7	92
5	3	70
6	8	95
7	2	65
8	5	80
9	6	85
10	7	90

3. Análisis de Datos

Aplica técnicas estadísticas para analizar los datos. Esto puede incluir la creación de gráficos, cálculos de estadísticas descriptivas, y pruebas de hipótesis.

Ejemplo: Calcula la media, mediana y desviación estándar de las horas de estudio y las calificaciones.

• Media (Horas de Estudio): (5 + 6 + 4 + 7 + 3 + 8 + 2 + 5 + 6 + 7) / 10 = 5.3 horas
  Media (Calificaciones): (85 + 88 + 78 + 92 + 70 + 95 + 65 + 80 + 85 + 90) / 10 = 82.8

• Desviación Estándar (Horas de Estudio): √[(Σ(x – μ)²) / N] = 1.8
  Desviación Estándar (Calificaciones): √[(Σ(x – μ)²) / N] = 9.4

4. Interpretación de Resultados

Interpreta los resultados de tu análisis para responder la pregunta original y tomar decisiones informadas.

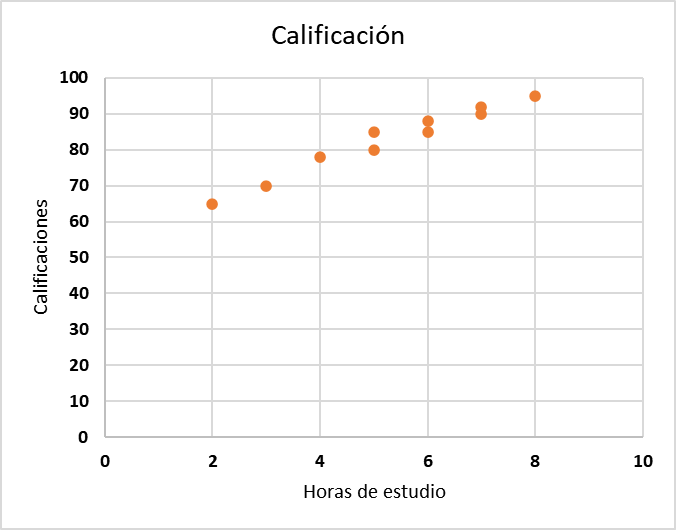
Ejemplo: Observa que hay una tendencia positiva entre las horas de estudio y las calificaciones, lo que sugiere que a más horas de estudio, mejores son las calificaciones.

5. Presentación de Soluciones

Comunica tus hallazgos de manera clara y coherente. Utiliza tablas, gráficos y resúmenes para presentar la información de manera accesible.

Ejemplo: Utiliza un gráfico de dispersión para mostrar la relación entre las horas de estudio y las calificaciones. El eje x representará las horas de estudio y el eje y representará las calificaciones. Añade una línea de tendencia para visualizar mejor la correlación.

Conclusión

Aplicando estas estrategias de resolución de problemas, serás capaz de abordar problemas estadísticos de manera sistemática y efectiva. Esto no solo mejorará tus habilidades analíticas, sino que también te permitirá tomar decisiones basadas en datos de manera más confiable.

Resources:

---

Learning activities:

Realiza un resumen de las estrategias de resolución de problemas indicado en esta unidad.

Considera utilizar un ejemplo con valores distintos a los presentados aquí.

Adaptaciones curriculares:

Explica oralmente a tu profesor lo entendido en esta lección.