Función logarítmica

¿Te has preguntado alguna vez cómo los matemáticos y científicos trabajan con números extremadamente grandes o pequeños? La función logarítmica es una herramienta esencial en las matemáticas que nos ayuda a entender y manejar estos números. Desde la medición de terremotos hasta el cálculo de intereses compuestos, las funciones logarítmicas son fundamentales para simplificar y resolver problemas complejos. En esta lección, exploraremos a fondo las funciones logarítmicas y descubriremos cómo se aplican en diferentes contextos.

---

Learning goals:

Al final de esta lección, tú serás capaz de:

1. Comprender el concepto y la definición de una función logarítmica.
2. Identificar y aplicar las propiedades de las funciones logarítmicas.
3. Representar gráficamente una función logarítmica y analizar sus características.
4. Resolver problemas y ecuaciones utilizando funciones logarítmicas.
5. Aplicar funciones logarítmicas en situaciones prácticas y contextos de la vida diaria.

---

Función Logarítmica: Definición y Propiedades

Definición

Una función logarítmica es una función del tipo f(x)=log⁡b(x)f(x) = \log_b(x), donde bb es la base del logaritmo y xx es el argumento. La base bb debe ser un número positivo distinto de 1.

Propiedades de las Funciones Logarítmicas

1. Dominio y Rango:
   • Dominio: x>0
   • Rango: (−∞,∞)
2. Intersección con el Eje Y:
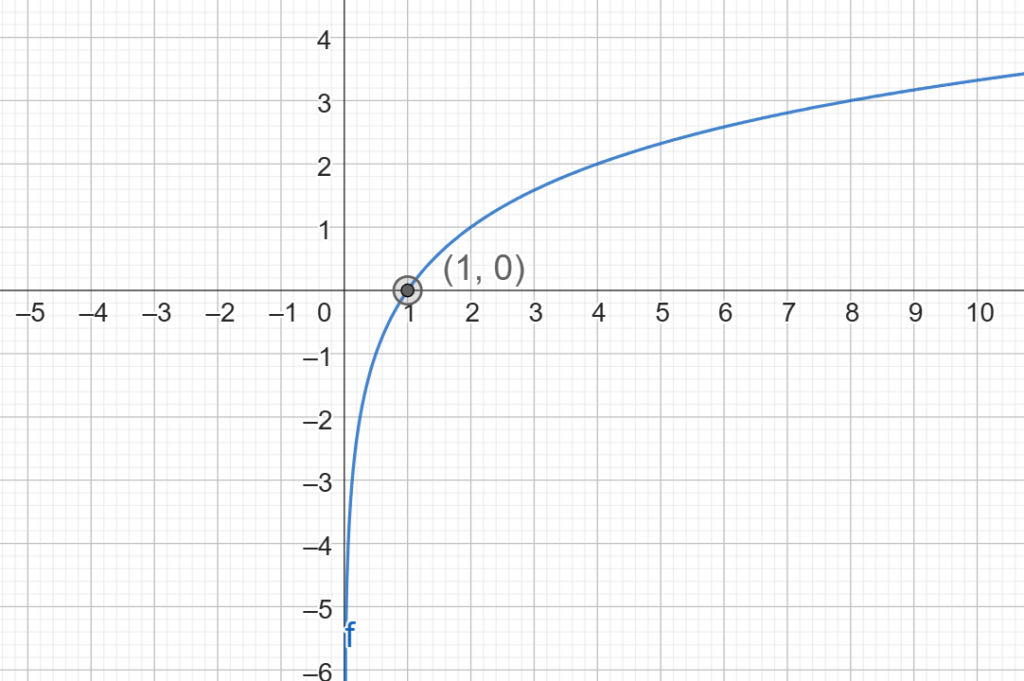
   • La función log⁡_b(x) intercepta el eje y en el punto (1, 0).
3. Comportamiento Asintótico:
   • La función tiene una asíntota vertical en x=0.
4. Crecimiento y Decrecimiento:
   • Si b>1, la función log⁡_b(x) es creciente.
   • Si 0<b<1, la función log⁡_b(x) es decreciente.
5. Inversa:
   • La inversa de la función logarítmica f(x)=log⁡_b(x) es la función exponencial g(x)=b^x.

Ejercicios Resueltos

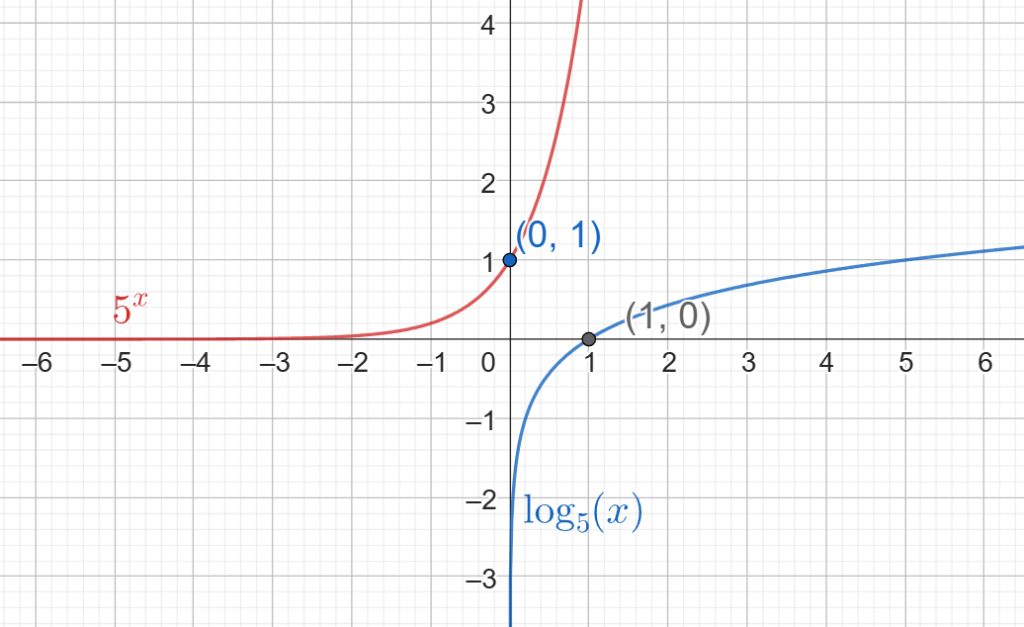
Resources:

---

Learning activities:

Ejercicios propuestos:

Actividades Lúdicas para el Aula

1. Juego de Tarjetas de Funciones Logarítmicas:
   • Crea tarjetas con diferentes funciones logarítmicas y sus propiedades. Los estudiantes deben unir las tarjetas correspondientes.
2. Bingo de Funciones Logarítmicas:
   • Crea tarjetas de bingo con diferentes características de funciones logarítmicas (dominio, rango, inversa, etc.). A medida que se leen las descripciones, los estudiantes deben identificar la característica correcta en sus tarjetas de bingo.
3. Competencia de Resolución de Problemas:
   • Organiza una competencia donde los estudiantes, en equipos, deben resolver problemas relacionados con funciones logarítmicas lo más rápido posible. Proporciona puntos por cada respuesta correcta y premia al equipo con más puntos.
4. Rompecabezas de Funciones Logarítmicas:
   • Proporciona piezas de rompecabezas con diferentes funciones logarítmicas y sus gráficos. Los estudiantes deben unir correctamente las piezas para completar el rompecabezas.
5. Escape Room de Funciones Logarítmicas:
   • Crea una serie de pistas y problemas relacionados con funciones logarítmicas que los estudiantes deben resolver para avanzar a la siguiente pista y finalmente “escapar” del aula. Divide a los estudiantes en equipos y dales un tiempo límite para completar todas las pistas.

Adaptaciones curriculares:

Permitir resolver pero no graficar, o proporcionar las gráficas y solicitar que se determine el dominio y rango aproximados con ayuda de la observación directa.